题目内容
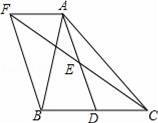
如图，在梯形ABCD中，AD∥BC，AC，BD交于点O，S
△AOD：S△COB=1：9，则S△DOC：S△BOC= ．
1：3 ．
【考点】相似三角形的判定与性质；梯形．
【专题】压轴题．
【分析】根据在梯形ABCD中，AD∥BC，AC，易得△AOD∽△COB，且S△AOD：S△COB=1：9，可求
=
，则S△AOD：S△DOC=1：3，所以S△DOC：S△BOC=1：3．
【解答】解：根据题意，AD∥BC
∴△AOD∽△COB
∵S△AOD：S△COB=1：9
∴=
则S△AOD：S△DOC=1：3
所以S△DOC：S△BOC=3：9=1：3．
【点评】本题主要考查了相似三角形的性质，相似三角形面积的比等于相似比的平方．
练习册系列答案
相关题目
5年这两年的平均增长率为x，则下列方程正确的是（ ）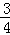
x2+mx+n经过点A和点C．且与x轴交于点B，动点P在x轴上以每秒1个单位长度的速度由点B向点A运动．点Q由点C沿线段CA向点A运动．且速度是点P运动速度的2倍．
