题目内容
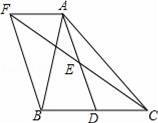
如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.
(1)BD与CD有什么数量关系,并说明理由;
(2)当△ABC满足什么条件时,四边形AFBD是矩形?并说明理由.
(3)在(2)的条件下,△ABC满足条件 ,矩形AFBD是正方形.

【考点】正方形的判定;全等三角形的判定与性质;矩形的判定.
【分析】(1)根据两直线平行,内错角相等求出∠AFE=∠DCE,然后利用“角角边”证明△AEF和△DEC全等,根据全等三角形对应边相等可得AF=CD,再利用等量代换即可得证;
(2)先利用一组对边平行且相等的四边形是平行四边形证明四边形AFBD是平行四边形,再根据一个角是直角的平行四边形是矩形,可知∠ADB=90°,由等腰三角形三线合一的性质可知必须是AB=AC.
(3)添加∠BAC=90°,根据直角三角形的性质:斜边中线等于斜边的一半可得AD=BD,进而可得矩形AFBD是正方形.
【解答】解:(1)BD=CD,
理由:∵AF∥BC,
∴∠AFE=∠DCE,
∵E是AD的中点,
∴AE=DE,
在△AEF和△DEC中,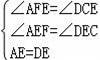
 ,
,
∴△AEF≌△DEC(AAS),
∴AF=CD,
∴AF=BD,
∴DB=CD;
(2)当△ABC满足:AB=AC时,四边形AFBD是矩形.
理由如下:∵AF∥BD,AF=BD,
∴四边形AFBD是平行四边形,
∵AB=AC,BD=CD(三线合一),
∴∠ADB=90°,
∴▱AFBD是矩形.
(3)△ABC满足∠BAC=90°,矩形AFBD是正方形;
∵BD=CD,∠BAC=90°,
∴AD=BD,
∴矩形AFBD是正方形.
【点评】本题考查了矩形、正方形的判定,全等三角形的判定与性质,平行四边形的判定,明确有一个角是直角的平行四边形是矩形是解本题的关键.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 .
. 
 △AOD:S△COB=1:9,则S△DOC:S△BOC= .
△AOD:S△COB=1:9,则S△DOC:S△BOC= .

 ,则AB的长是 .
,则AB的长是 .




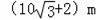
 B.
B.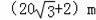

 D.
D.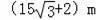
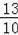
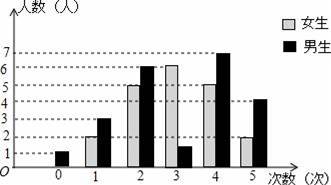
 ,男生收看“两会”新闻次数的方差为2,请比较该班级男、女生收看“两会”新闻次数的波动大小.
,男生收看“两会”新闻次数的方差为2,请比较该班级男、女生收看“两会”新闻次数的波动大小.