题目内容
响应政府“节能”号召,我市华强照明公司减少了白炽灯的生产数量,引进新工艺生产一种新型节能灯,已知这种节能灯的出厂价为每个10元.某商场试销发现,销售单价定为15元/个,每月销售量为350个;每涨价1元,每月少卖10个.
(1)求出每月销售量y(个)与销售单价x(元)之间的函数关系,并写出自变量的取值范围;
(2)设该商场每月销售这种节能灯获得的利润为w(元),当销售单价定为多少元时,每月可获得最大利润?
【考点】二次函数的应用.
【分析】(1)首先表示出销售单价x元时涨价(x﹣10)元,每涨价1元,每月少卖10个,则少买10(x﹣15),表示出y即可;
(2)由总利润=销售量•每件纯赚利润,得w=(x﹣10)(﹣10x+500),把函数转化成顶点坐标式,根据二次函数的性质求出 最大利润.
最大利润.
【解答】解:(1)由题意得:y=350﹣10(x﹣15)=﹣10x+500(15≤x≤50);
(2)依题意得:w=(x﹣10)(﹣10x+500)
=﹣10(x﹣30)2+4000,
∵﹣10<0 ,
,
∴当x=30时,w有最大值=4000.
答:当定价定为30元时,每月可获得最大利润4000元.
【点评】本题主要考查了二次函数的应用的知识点,解答本题的关键熟练掌握二次函数的性质以及二次函数最大值的求解.

练习册系列答案
相关题目
 .
. 

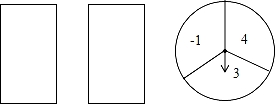
 方形ABOC的边长是2,反比例函数y=
方形ABOC的边长是2,反比例函数y=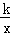 (x≠0)图象经过点A,则k的值是( )
(x≠0)图象经过点A,则k的值是( )
 △AOD:S△COB=1:9,则S△DOC:S△BOC= .
△AOD:S△COB=1:9,则S△DOC:S△BOC= .
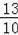
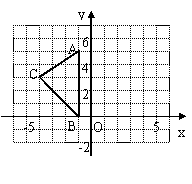
 ,男生收看“两会”新闻次数的方差为2,请比较该班级男、女生收看“两会”新闻次数的波动大小.
,男生收看“两会”新闻次数的方差为2,请比较该班级男、女生收看“两会”新闻次数的波动大小.