题目内容
12.把一个自然数所有数位上的数字先平方再求和得到一个新数,叫做第一次运算,再把所得新数所有数位上的数字先平方再求和又将得到一个新数,叫做第二次运算,…如此重复下去,若最终结果为1,我们把具有这种特征的自然数称为“快乐数”.例如:32→32+22=13→12+32=10→12+02=1,
70→72+02=49→42+92=97→92+72=130→12+32+02=10→12+02=1,
所以32和70都是“快乐数”.
(1)写出最小的两位“快乐数”;判断19是不是“快乐数”;请证明任意一个“快乐数”经过若干次运算后都不可能得到4;
(2)若一个三位“快乐数”经过两次运算后结果为1,把这个三位“快乐数”与它的各位上的数字相加所得的和被8除余数是2,求出这个“快乐数”.
分析 (1)根据“快乐数”的定义计算即可;
(2)设三位“快乐数”为100a+10b+c,根据“快乐数”的定义计算.
解答 解:(1)∵12+02=1,
∴最小的两位“快乐数”10,
∵19→12+92=82→82+22=68→62+82=100→12+02+02=1,
∴19是快乐数;
证明:∵4→16→37→58→89→145→42→20→4,
4出现两次,所以后面将重复出现,永远不会出现1,
所以任意一个“快乐数”经过若干次运算后都不可能得到4.
(2)设三位“快乐数”为100a+10b+c,由题意,经过两次运算后结果为1,所以第一次运算后结果一定是10或者100,
则a2+b2+c2=10或100,
∵a、b、c为整数,且a≠0,
∴当a2+b2+c2=10时,12+32+02=10,
①当a=1,b=3或0,c=0或3时,三位“快乐数”为130,103,
②当a=2时,无解;
③当a=3,b=1或0,c=0或1时,三位“快乐数”为310,301,
同理当a2+b2+c2=100时,62+82+02=100,
所以三位“快乐数”有680,608,806,860.
综上一共有130,103,310,301,680,608,806,860八个,
又因为三位“快乐数”与它的各位上的数字相加所得的和被8除余数是2,所以只有310和860满足已知条件.
点评 本题考查的是因式分解的定义、“快乐数”的定义,正确理解“快乐数”的定义、掌握分情况讨论思想是解题的关键.

练习册系列答案
相关题目
4.2015年4月30日新的津蓟铁路市郊列车取代了传统的绿皮车,实现列车升级,并且升级后列车从天津到蓟县的行驶路程比原路程缩短25公里,实现升级后列车的行驶速度是原来速度的$\frac{10}{7}$倍,从天津到蓟县的行驶时间缩短了1小时.若列车升级前绿皮车从天津到蓟县的行驶路程为175公里,则列车升级后的速度为( )
| A. | 45公里/小时 | B. | 60公里/小时 | C. | 90公里/小时 | D. | 100公里/小时 |
2.在某一时刻,测得一根高为1.8m的竹竿的影长为3m,同时测得一根旗杆的影长为25m,那么这根旗杆的高度为( )
| A. | 8m | B. | 10m | C. | 15m | D. | 20m |
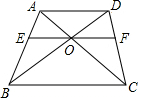 四边形ABCD中,AD∥BC,AC与BD相交于O点,过O点作EF∥BC分别交AB、CD于E,F两点,求证:
四边形ABCD中,AD∥BC,AC与BD相交于O点,过O点作EF∥BC分别交AB、CD于E,F两点,求证: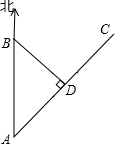 如图所示,沿海城市B的正南方向A处有一台风中心,沿AC的方向以30km/h的速度移动3小时后到达D处.已知A距台风中心最短的距离BD为120km,求AB间的距离.
如图所示,沿海城市B的正南方向A处有一台风中心,沿AC的方向以30km/h的速度移动3小时后到达D处.已知A距台风中心最短的距离BD为120km,求AB间的距离. 如图,一个直立的油桶高0.8米,在顶部的一个开口中将一根长1米的木杆斜着插入桶内,上端正好与桶面相平,抽出后看到杆上油浸到部分长0.8m,则油桶内油面的高度是0.64m.
如图,一个直立的油桶高0.8米,在顶部的一个开口中将一根长1米的木杆斜着插入桶内,上端正好与桶面相平,抽出后看到杆上油浸到部分长0.8m,则油桶内油面的高度是0.64m.