题目内容
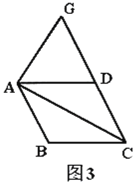
【题目】如图，折线
中，
，
，将折线绕点
按逆时针方向旋转，得到折线
，点
的对应点落在线段
上的点
处，点
的对应点落在点
处，连接
，若
，则
_____°．
【答案】
【解析】
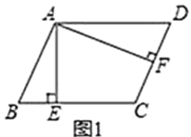
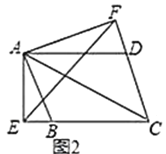
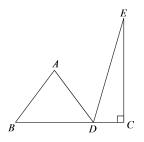
连接AC 、AE ，过点A作AF⊥BC于F ,作AH⊥EC于H．再证明四边形AFCH是矩形,可得AF=CH ,由旋转的性质可得AD=AB=3、BC=DE=5，∠ABC=∠ADE，则△ABC≌△ADE，即AC=AE ；再由等腰三角形的性质和勾股定理可得BF、AF、EC、CD的长，最后根据正切定义解答即可．
解：如图：连接AC 、AE ，过点A作AF⊥BC于F ,作AH⊥EC于H．
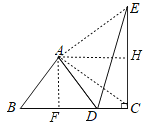
∵CE⊥BC，AF⊥BC，AH⊥EC
∴四边形AFCH是矩形，
∴AF=CH，
∵将折线AB-BC绕点A按逆时针方向旋转，得到折线AD-DE
∴AD=AB=3、BC=DE=5，∠ABC=∠ADE
∴△ABC≌△ADE
∴AC=AE，
∵AC=AE，AB=AD，AF⊥BC，AH⊥EC，BF=DF，CH=EH
∴
∴
∴BF=
，AF=
∴
∴
故答案为：2
练习册系列答案
相关题目
