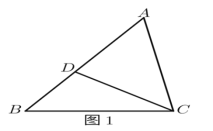
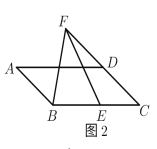
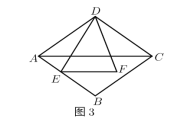
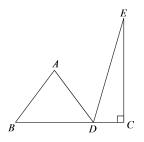
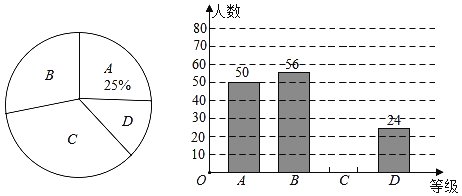
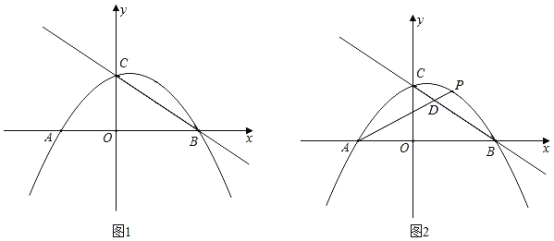
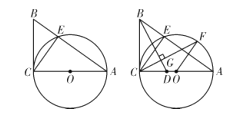
ЬтФПФкШн
ЁОЬтФПЁПШчЭМЂйЃЌ![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЎЖЏЕу
ЃЎЖЏЕу![]() дк
дк![]() ЕФБпЩЯАД
ЕФБпЩЯАД![]() ЕФТЗЯпдШЫйвЦЖЏЃЌЕБЕу
ЕФТЗЯпдШЫйвЦЖЏЃЌЕБЕу![]() ЕНДя
ЕНДя![]() ЕуЪБЭЃжЙвЦЖЏЃЛЖЏЕу
ЕуЪБЭЃжЙвЦЖЏЃЛЖЏЕу![]() вд
вд![]() ЕФЫйЖШдк
ЕФЫйЖШдк![]() ЕФБпЩЯАД
ЕФБпЩЯАД![]() ЕФТЗЯпдШЫйвЦЖЏЃЌЕБЕу
ЕФТЗЯпдШЫйвЦЖЏЃЌЕБЕу![]() ЕНДя
ЕНДя![]() ЕуЪБЭЃжЙвЦЖЏЃЎвбжЊЕу
ЕуЪБЭЃжЙвЦЖЏЃЎвбжЊЕу![]() ЁЂЕу
ЁЂЕу![]() ЭЌЪБПЊЪМвЦЖЏЃЌЭЌЪБЭЃжЙвЦЖЏ(МДЭЌЪБЕНДяИїздЕФжежЙЮЛжУ)ЃЎЩшЖЏЕу
ЭЌЪБПЊЪМвЦЖЏЃЌЭЌЪБЭЃжЙвЦЖЏ(МДЭЌЪБЕНДяИїздЕФжежЙЮЛжУ)ЃЎЩшЖЏЕу![]() вЦЖЏЕФЪБМфЮЊ
вЦЖЏЕФЪБМфЮЊ![]() ЃЌ
ЃЌ![]() ЕФУцЛ§ЮЊ
ЕФУцЛ§ЮЊ![]() ЃЌ
ЃЌ![]() гы
гы![]() ЕФКЏЪ§ЙиЯЕШчЭМЂкЫљЪОЃЎ
ЕФКЏЪ§ЙиЯЕШчЭМЂкЫљЪОЃЎ
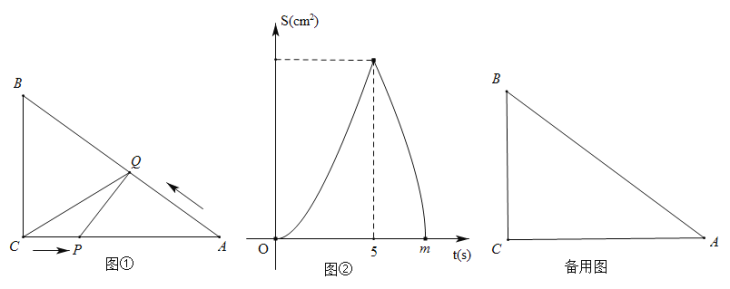
(1)ЭМЂйжа![]() ЁЁЁЁ
ЁЁЁЁ![]() ЃЌЭМЂкжа
ЃЌЭМЂкжа![]() ЁЁЁЁ
ЁЁЁЁ![]() ЃЛ
ЃЛ
(2)Чѓ![]() гы
гы![]() ЕФКЏЪ§БэДяЪНЃЛ
ЕФКЏЪ§БэДяЪНЃЛ
(3)ЕБ![]() ЮЊКЮжЕЪБЃЌ
ЮЊКЮжЕЪБЃЌ![]() ЮЊЕШбќШ§НЧаЮЃЎ
ЮЊЕШбќШ§НЧаЮЃЎ
ЁОД№АИЁПЃЈ1ЃЉ10ЃЌ15ЃЛЃЈ2ЃЉМћЯъНтЃЛЃЈ3ЃЉМћЯъНт
ЁОНтЮіЁП
![]() ЃЌИљОн
ЃЌИљОн![]() ЃЌ
ЃЌ![]() ЃЌЕУЕН
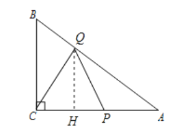
ЃЌЕУЕН![]() ЃЌНјЖјЕУЕНЖЏЕуPЕФЫйЖШЮЊЃК
ЃЌНјЖјЕУЕНЖЏЕуPЕФЫйЖШЮЊЃК ЃЌМДПЩЕУЕН
ЃЌМДПЩЕУЕН![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЕБ![]() ЪБЃЌЙ§Еу
ЪБЃЌЙ§Еу![]() зї
зї![]() ЃЌДЙзуЮЊ
ЃЌДЙзуЮЊ![]() ЃЌИљОн
ЃЌИљОн![]() ЃЌЕУЕН
ЃЌЕУЕН![]() ЃЌ
ЃЌ![]() ЃЌНјЖјЕУЕН
ЃЌНјЖјЕУЕН![]() ЃЌ
ЃЌ![]() ЃЛЕБ
ЃЛЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЛ
ЃЛ
ЃЈ3ЃЉЕБ![]() ЪБЃЌЕу
ЪБЃЌЕу![]() дк
дк![]() ЩЯЃЌИљОн
ЩЯЃЌИљОн![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌШє
ЃЌШє![]() ЮЊЕШбќШ§НЧаЮЃЌдђ
ЮЊЕШбќШ§НЧаЮЃЌдђ![]() ЃЌИљОн
ЃЌИљОн![]() ЃЌ
ЃЌ![]() ЃЌЕУЕН
ЃЌЕУЕН![]() ЃЌИљОн
ЃЌИљОн![]() МДПЩЧѓНтЃЛЕБ
МДПЩЧѓНтЃЛЕБ![]() ЪБЃЌЕу
ЪБЃЌЕу![]() дк
дк![]() ЩЯЃЌИљОн
ЩЯЃЌИљОн![]() ЃЌШє
ЃЌШє![]() ЮЊЕШбќШ§НЧаЮЃЌдђ
ЮЊЕШбќШ§НЧаЮЃЌдђ![]() ЃЌЕУЕН
ЃЌЕУЕН![]() ЃЌМДПЩЧѓНтЃЎ
ЃЌМДПЩЧѓНтЃЎ
НтЃКЃЈ1ЃЉ![]()
Ёп![]() ЃЌ
ЃЌ![]()
Ёр![]()
ЁрЖЏЕуPЕФЫйЖШЮЊЃК
Ёр![]()
ЙЪД№АИЮЊЃК10ЃЌ15ЃЎ
ЃЈ2ЃЉЕБ![]() ЪБЃЌЙ§Еу
ЪБЃЌЙ§Еу![]() зї
зї![]() ЃЌДЙзуЮЊ
ЃЌДЙзуЮЊ![]() ЃЌ
ЃЌ
Ёп![]()
Ёр![]()
Ёр![]()
Ёр![]()
Ёр![]()
Ёр![]() ЃЛ
ЃЛ
ЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЛ
ЃЛ
ЃЈ3ЃЉЕБ![]() ЪБЃЌЕу
ЪБЃЌЕу![]() дк
дк![]() ЩЯ.
ЩЯ.
![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() Шє
Шє![]() ЮЊЕШбќШ§НЧаЮЃЌдђ
ЮЊЕШбќШ§НЧаЮЃЌдђ![]() .
.
![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() .
.
![]() ЃЌ
ЃЌ![]() ЃЛ
ЃЛ
ЕБ![]() ЪБЃЌЕу
ЪБЃЌЕу![]() дк
дк![]() ЩЯ.
ЩЯ.
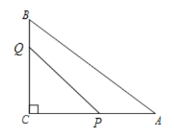
![]() ,
,![]() Шє
Шє![]() ЮЊЕШбќШ§НЧаЮЃЌдђ
ЮЊЕШбќШ§НЧаЮЃЌдђ![]() .
.
![]() ЃЌ
ЃЌ![]() .
.

 аЁбЇНЬВФЭъШЋНтЖСЯЕСаД№АИ
аЁбЇНЬВФЭъШЋНтЖСЯЕСаД№АИЁОЬтФПЁПЖўДЮКЏЪ§![]() ЃЈ
ЃЈ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЪЧГЃЪ§ЃЌ
ЪЧГЃЪ§ЃЌ![]() ЃЉЕФздБфСПxгыКЏЪ§жЕyЕФВПЗжЖдгІжЕШчЯТБэЃК
ЃЉЕФздБфСПxгыКЏЪ§жЕyЕФВПЗжЖдгІжЕШчЯТБэЃК
| Ё | -1 | 0 | 1 | 3 | Ё |
| Ё |
| 3 |
| 3 | Ё |
ЧвЕБ![]() ЪБЃЌгыЦфЖдгІЕФКЏЪ§жЕ
ЪБЃЌгыЦфЖдгІЕФКЏЪ§жЕ![]() ЃЎгаЯТСаНсТлЃКЂй
ЃЎгаЯТСаНсТлЃКЂй![]() ЃЛЂк3ЪЧЙигк
ЃЛЂк3ЪЧЙигк![]() ЕФЗНГЬ
ЕФЗНГЬ![]() ЕФвЛИіИљЃЛЂл
ЕФвЛИіИљЃЛЂл![]() ЃЎЦфжаЃЌе§ШЗНсТлЕФИіЪ§ЪЧЃЈ ЃЉ
ЃЎЦфжаЃЌе§ШЗНсТлЕФИіЪ§ЪЧЃЈ ЃЉ
A.0B.1C.2/span>D.3