题目内容
3．已知（x-1）（x+2）=ax2+bx+c，则代数式4a-2b+c的值为0．分析 首先利用多项式的乘法法则，然后根据多项式相等，则对应项的系数相等，据此求得a、b、c的值，然后代入求值即可．
解答 解：（x-1）（x+2）
=x2-x+2x-2
=x2+x-2
=ax2+bx+c，
则a=1，b=1，c=-2．
故原式=4-2-2=0．
故答案是：0．
点评 本题考查了多项式乘法法则以及多项式相等的条件，正确理解多项式的乘法法则是关键．
练习册系列答案
相关题目
13．若（x+2）（x-a）=x2+bx-10，则b的值为（ ）
| A． | -3 | B． | 3 | C． | -5 | D． | 5 |
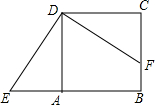如图，正方形ABCD中，点F在边BC上，E在边BA的延长线上，△DCF按顺时针方向旋转后恰好与△DAE重合，若AE=3，BF=2，则四边形BFDE的面积是25．
18．如果（x+q）（x+5）=px2+7x+10，则q与p的值分别是（ ）
| A． | 5、2 | B． | 1、5 | C． | 2、1 | D． | 2、5 |
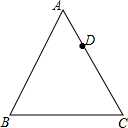如图，点D在边长为6的等边△ABC的边AC上，且AD=2，将△ABC绕点C顺时针方向旋转60°，若此时点A和点D的对应点分别记作点E和点F，联结BF交边AC与点G，那么tan∠AEG=$\frac{3\sqrt{3}}{7}$．
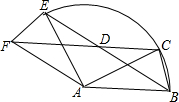如图，△ABC中，AB=AC=2，∠BAC=30°，△AEF是由△ABC绕点A按逆时针方向旋转得到的，连接BE、CF相交于点D，$\widehat{BE}$是点B旋转形成的弧．
13．下列图形不是轴对称图形的是（ ）
| A． | 正方形 | B． | 等腰三角形 | C． | 圆 | D． | 平行四边形 |