题目内容
11.[x]表示不超过x的最大整数,如[3.15]=3,[-2.7]=-3,[4]=4,则$\frac{[\sqrt{1×2}]+[\sqrt{2×3}]+…+[\sqrt{2015×2016}]}{2015}$=1008.分析 根据[x]表示不大于x的最大整数可得到[$\sqrt{1×2}$]=1,[$\sqrt{2×3}$]=2,[$\sqrt{\sqrt{3×4}}$]=3,…,[$\sqrt{2015×2016}$]=2015,然后计算$\frac{1+2+3+…+2015}{2015}$即可.
解答 解:∵[$\sqrt{1×2}$]=1,[$\sqrt{2×3}$]=2,[$\sqrt{\sqrt{3×4}}$]=3,…,[$\sqrt{2015×2016}$]=2015,
∴原式=$\frac{1+2+3+…+2015}{2015}$=$\frac{\frac{1}{2}×(1+2015)×2015}{2015}$=1008.
故答案为:1008.
点评 本题考查了取整计算:[x]表示不大于x的最大整数,如[3.15]=3,[-2.7]=-3,[4]=4.

练习册系列答案
相关题目
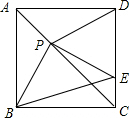 如图,正方形ABCD中,对角线AC上有一点P,连接BP、DP,过点P作PE⊥PB交CD于点E,连接BE.
如图,正方形ABCD中,对角线AC上有一点P,连接BP、DP,过点P作PE⊥PB交CD于点E,连接BE.