题目内容
14．若三角形的各边长均为正整数，且最长边为9，则这样的三角形的个数是多少？分析 确定三边中的两边，分类找到边长是整数，且最长边为9的三角形的个数即可．
解答 解：当2边长分别为9，9时，第3边可取1，2，3，4，5，…，9，这样的三角形有9种；
当2边长为8，9时，第3边可取2，3，4，5，…8，这样的三角形有7种；
当2边长为7，9时，第3边可取3，4，5，6，7，这样的三角形有5种；
当2边长为6，9时，第3边可取4，5，6，这样的三角形有3种；
当2边长为5，9时，第3边可取5，这样的三角形有1种；
这样的三角形共有9+7+5+3+1=25（个）．
点评 本题考查了三角形的三边关系，属于基础题，解决本题的关键是分类得到三角形的三边长；注意去掉重合的组成三角形的三边．
练习册系列答案
名师导航单元期末冲刺100分系列答案
名校名卷单元同步训练测试题系列答案
相关题目
二次函数y=x2-8x+n的部分图象如图所示，若关于x的一元二次方程x2-8x+n=0的一个解为x1=1．则另一个解为x2=7．
2．已知二次函数y=2mx2+（4m-1）x-1与x轴交点的横坐标为x1，x2，且x1＜x2，则下列结论中：
①方程2mx2+（4m-1）x-1=0有两个不相等的实数根x1，x2；
②当x=-2时，y=1；
③当x＜x1时，y＞0；
④x1＜-1，x2＞-1．
其中正确的结论是（ ）
①方程2mx2+（4m-1）x-1=0有两个不相等的实数根x1，x2；
②当x=-2时，y=1；
③当x＜x1时，y＞0；
④x1＜-1，x2＞-1．
其中正确的结论是（ ）
| A． | ①③④ | B． | ①② | C． | ①②③ | D． | ①②④ |
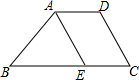如图，梯形ABCD的上底AD=3，下底BC=8，腰CD=4，求另一腰AB的取值范围．
6．下列各数中，没有平方根的是（ ）
| A． | |-3| | B． | -（-3） | C． | -32 | D． | （-3）2 |
