题目内容
17.先化简,后求值:$\frac{{x}^{3}-4{x}^{2}+4x}{{x}^{2}-2x}$,其中x=$\sqrt{2}$-2.分析 先分子、分母分解因式,再约分,最后代入求出即可.
解答 解:$\frac{{x}^{3}-4{x}^{2}+4x}{{x}^{2}-2x}$
=$\frac{x(x-2)^{2}}{x(x-2)}$
=x-2,
当x=$\sqrt{2}$-2时,原式=$\sqrt{2}$-2-2=$\sqrt{2}$-4.
点评 本题考查了分式的混合运算和求值的应用,解此题的关键是能正确化简,难度不是很大.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
2.已知二次函数y=2mx2+(4m-1)x-1与x轴交点的横坐标为x1,x2,且x1<x2,则下列结论中:
①方程2mx2+(4m-1)x-1=0有两个不相等的实数根x1,x2;
②当x=-2时,y=1;
③当x<x1时,y>0;
④x1<-1,x2>-1.
其中正确的结论是( )
①方程2mx2+(4m-1)x-1=0有两个不相等的实数根x1,x2;
②当x=-2时,y=1;
③当x<x1时,y>0;
④x1<-1,x2>-1.
其中正确的结论是( )
| A. | ①③④ | B. | ①② | C. | ①②③ | D. | ①②④ |
6.下列各数中,没有平方根的是( )
| A. | |-3| | B. | -(-3) | C. | -32 | D. | (-3)2 |
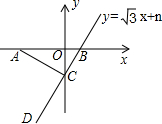 如图,点A的坐标为(-4,0),直线y=$\sqrt{3}$x+n与坐标轴交于点B、C,连接AC,如果∠ACD=90°,则n的值为$-\frac{4\sqrt{3}}{3}$.
如图,点A的坐标为(-4,0),直线y=$\sqrt{3}$x+n与坐标轴交于点B、C,连接AC,如果∠ACD=90°,则n的值为$-\frac{4\sqrt{3}}{3}$.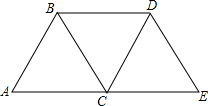 如图,把△ABC按AC方向平移,平移的距离是AC的长度,则平移后点B平移到点D,连接BD后,得到的四边形ACDB和CEDB都是平行四边形吗?
如图,把△ABC按AC方向平移,平移的距离是AC的长度,则平移后点B平移到点D,连接BD后,得到的四边形ACDB和CEDB都是平行四边形吗?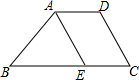 如图,梯形ABCD的上底AD=3,下底BC=8,腰CD=4,求另一腰AB的取值范围.
如图,梯形ABCD的上底AD=3,下底BC=8,腰CD=4,求另一腰AB的取值范围.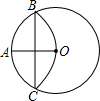 如图,⊙O的半径OA=6,以点A为圆心,OA为半径的弧交⊙O于B,C两点,求弦BC的长.
如图,⊙O的半径OA=6,以点A为圆心,OA为半径的弧交⊙O于B,C两点,求弦BC的长.