题目内容
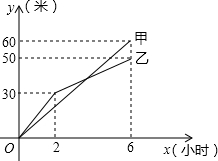 甲、乙两个工程队分别同时开挖两段河渠,所挖河渠的长度y(米)与挖掘时间x(小时)之间的关系如图所示,请根据图象判断下列信息正确的有( )
甲、乙两个工程队分别同时开挖两段河渠,所挖河渠的长度y(米)与挖掘时间x(小时)之间的关系如图所示,请根据图象判断下列信息正确的有( )①乙队开挖到30米,用了2小时.
②开挖6小时甲队比乙队多挖了10米.
③甲队在0≤x≤6的时段内,y与x的函数关系式为y=
| 1 |
| 10 |
④当x=4时,甲乙两队在施工过程中所挖河渠的长度相等.
| A、1个 | B、2个 | C、3个 | D、4个 |
考点:一次函数的应用
专题:
分析:①由函数图象可以得出乙队开挖到30米,用了2小时;
②由函数图象可以得出开挖6小时甲队比乙队多挖了10米;
③当0≤x≤6时,设甲队所挖河渠的长度y(米)与挖掘时间x(小时)之间的关系为y=kx,由待定系数法求出其解即可;
④当2≤x≤6时,设乙队所挖河渠的长度y(米)与挖掘时间x(小时)之间的关系为y1=k1x+b,由待定系数法求出其解即可.
②由函数图象可以得出开挖6小时甲队比乙队多挖了10米;
③当0≤x≤6时,设甲队所挖河渠的长度y(米)与挖掘时间x(小时)之间的关系为y=kx,由待定系数法求出其解即可;
④当2≤x≤6时,设乙队所挖河渠的长度y(米)与挖掘时间x(小时)之间的关系为y1=k1x+b,由待定系数法求出其解即可.
解答:解:①由函数图象可以得出乙队开挖到30米,用了2小时,故正确;
②由函数图象可以得出开挖6小时甲队比乙队多挖了10米,故正确;
③当0≤x≤6时,设甲队所挖河渠的长度y(米)与挖掘时间x(小时)之间的关系为y=kx,由题意,得
60=6k,
∴k=10,
∴y=10x.故错误;
④当2≤x≤6时,设乙队所挖河渠的长度y(米)与挖掘时间x(小时)之间的关系为y1=k1x+b,由题意,得
,
解得:
,
∴y1=5x+20.
当x=4时,y1=40,
y=40,
∴y1=y,
∴当x=4时,甲乙两队在施工过程中所挖河渠的长度相等,故正确.
综上所述:正确的有①②④共3个.
故选C.
②由函数图象可以得出开挖6小时甲队比乙队多挖了10米,故正确;
③当0≤x≤6时,设甲队所挖河渠的长度y(米)与挖掘时间x(小时)之间的关系为y=kx,由题意,得
60=6k,
∴k=10,
∴y=10x.故错误;
④当2≤x≤6时,设乙队所挖河渠的长度y(米)与挖掘时间x(小时)之间的关系为y1=k1x+b,由题意,得
|
解得:
|
∴y1=5x+20.
当x=4时,y1=40,
y=40,
∴y1=y,
∴当x=4时,甲乙两队在施工过程中所挖河渠的长度相等,故正确.
综上所述:正确的有①②④共3个.
故选C.
点评:本题考查了一次函数的图象的性质的运用,运用待定系数法求一次函数的解析式的运用,工程问题的数量关系的运用,解答时求出函数的解析式是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列各式
,
,
,
(x2+1),
中,是分式的共有( )
| a-b |
| 2 |
| x+3 |
| x |
| 5+y |
| π |
| ||
| 4 |
| a+b |
| a-b |
| A、1个 | B、2个 | C、3个 | D、4个 |
 已知:如图,在Rt△ABC中,AB=BC,在Rt△ADE中,AD=DE,且D在边AB上,连结EC,取EC的中点M,连结DM和BM,将直角三角形ADE绕A点按逆时针旋转45°,结论:△BMD为等腰直角三角形,成立吗?
已知:如图,在Rt△ABC中,AB=BC,在Rt△ADE中,AD=DE,且D在边AB上,连结EC,取EC的中点M,连结DM和BM,将直角三角形ADE绕A点按逆时针旋转45°,结论:△BMD为等腰直角三角形,成立吗?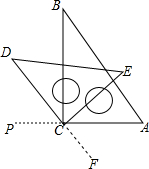 小明用一副三角板自制对顶角的“小仪器”,第一步固定直角三角板ABC,并将边AC延长至点P,第二步将另一块三角板CDE的直角顶点与三角板ABC的直角顶点C重合,摆放成如图所示,延长DC至点F,∠PCD与∠ACF就是一组对顶角.
小明用一副三角板自制对顶角的“小仪器”,第一步固定直角三角板ABC,并将边AC延长至点P,第二步将另一块三角板CDE的直角顶点与三角板ABC的直角顶点C重合,摆放成如图所示,延长DC至点F,∠PCD与∠ACF就是一组对顶角.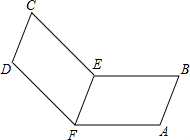 如图,取一张长方形的硬纸板ABCD,将硬纸板ABCD对折使CD与AB重合,EF为折痕.把长方形ABEF平放在桌面上,另一个面CDEF无论怎么改变位置总有CD∥AB存在,你知道为什么吗?
如图,取一张长方形的硬纸板ABCD,将硬纸板ABCD对折使CD与AB重合,EF为折痕.把长方形ABEF平放在桌面上,另一个面CDEF无论怎么改变位置总有CD∥AB存在,你知道为什么吗?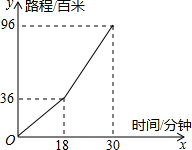 “懒洋洋”由于身体太胖,决定每天早上起来锻炼身体,帮助减肥,已知“懒洋洋”从“羊村”出发到森林里,先上坡后下坡,行程状况如图所示;若返回时上坡和下坡的速度扔保持不变,那么“懒洋洋”从森林到“羊村”所用的时间是
“懒洋洋”由于身体太胖,决定每天早上起来锻炼身体,帮助减肥,已知“懒洋洋”从“羊村”出发到森林里,先上坡后下坡,行程状况如图所示;若返回时上坡和下坡的速度扔保持不变,那么“懒洋洋”从森林到“羊村”所用的时间是