题目内容
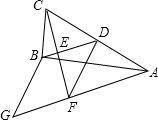 如图,在△ABC中,∠ABC=90°,BD为AC的中线,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接BG、DF.若
如图,在△ABC中,∠ABC=90°,BD为AC的中线,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接BG、DF.若| GF |
| AF |
| 5 |
| 8 |
考点:菱形的判定与性质,直角三角形斜边上的中线
专题:
分析:首先可判断四边形BGFD是平行四边形,再由直角三角形斜边中线等于斜边一半,可得BD=FD,则可判断四边形BGFD是菱形,设GF=x,则AF=13x,AC=2x,在Rt△ACF中利用勾股定理可求出x的值.
解答:解∵AG∥BD,BD=FG,
∴四边形BGFD是平行四边形,
∵CF⊥BD,
∴CF⊥AG,
又∵点D是AC中点,
∴BD=DF=
AC=5,
∴四边形BGFD是菱形.
∵
=
,CF=6,
∴GF=5x,则AF=8x,AC=10x,在Rt△ACF中利用勾股定理得到:100x2=64x2+36.
解得x2=1,则x=1(舍去负值).
则GF=5x=5.
故四边形BDFG的周长=4GF=20.
故答案是:20.
∴四边形BGFD是平行四边形,
∵CF⊥BD,

∴CF⊥AG,
又∵点D是AC中点,
∴BD=DF=
| 1 |
| 2 |
∴四边形BGFD是菱形.
∵
| GF |
| AF |
| 5 |
| 8 |
∴GF=5x,则AF=8x,AC=10x,在Rt△ACF中利用勾股定理得到:100x2=64x2+36.
解得x2=1,则x=1(舍去负值).
则GF=5x=5.
故四边形BDFG的周长=4GF=20.
故答案是:20.
点评:本题考查了菱形的判定与性质、勾股定理及直角三角形的斜边中线的性质,解答本题的关键是判断出四边形BGFD是菱形.

练习册系列答案
相关题目
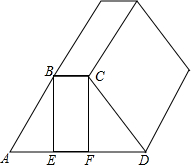 梯形ABCD是一段公路路基的截面图,现在需要在2个斜坡面植草,已知∠A=45°,DE=8m,DF=6m,路基长30m,每平方米的草坪的费用为a元,求2个斜坡面植草的总费用.
梯形ABCD是一段公路路基的截面图,现在需要在2个斜坡面植草,已知∠A=45°,DE=8m,DF=6m,路基长30m,每平方米的草坪的费用为a元,求2个斜坡面植草的总费用.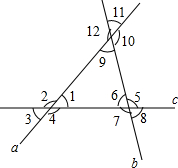 如图所示,a、b两条直线交于一点,生成∠9,探索∠9与原有角的位置关系.
如图所示,a、b两条直线交于一点,生成∠9,探索∠9与原有角的位置关系. 如图,边长为5的菱形ABCD中,AE⊥BC于点E,且AE=4.以AE为边向右作正方形AEFG.边GF与CD交于点H.
如图,边长为5的菱形ABCD中,AE⊥BC于点E,且AE=4.以AE为边向右作正方形AEFG.边GF与CD交于点H.
 如图,平行四边形ABCD中,E是边BC上的点,AE交BD于点F,如果
如图,平行四边形ABCD中,E是边BC上的点,AE交BD于点F,如果