题目内容
如图，平行四边形ABCD中，E是边BC上的点，AE交BD于点F，如果| BE |
| EC |
| BF |
| FD |
考点：平行四边形的性质,相似三角形的判定与性质
专题：
分析：由四边形ABCD是平行四边形，易得△BEF∽△DAF，即可得
=
，然后由
=2，求得答案．
| BF |
| FD |
| BE |
| AD |
| BE |
| EC |
解答：解：∵四边形ABCD是平行四边形，
∴AD∥BC，AD=BC，
∴△BEF∽△DAF，
∴
=
，
∵
=2，
∴
=
=
，
∴
=
．
故答案为：
．
∴AD∥BC，AD=BC，
∴△BEF∽△DAF，
∴
| BF |
| FD |
| BE |
| AD |
∵
| BE |
| EC |
∴
| BE |
| AD |
| BE |
| BC |
| 2 |
| 3 |
∴
| BF |
| FD |
| 2 |
| 3 |
故答案为：
| 2 |
| 3 |
点评：此题考查了平行四边形的性质以及相似三角形的判定与性质．此题难度不大，注意掌握数形结合思想的应用．
练习册系列答案
相关题目
如图，在△ABC中，∠ABC=90°，BD为AC的中线，过点C作CE⊥BD于点E，过点A作BD的平行线，交CE的延长线于点F，在AF的延长线上截取FG=BD，连接BG、DF．若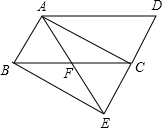
如图，将平行四边形ABCD的边DC延长到点E，使CE=DC，连接AE，交BC于点F．一元二次方程（m-2）x2-4mx+2m-6=0有两个相等的实数根，则m等于（ ）
| A、-6或1 | B、1 | C、-6 | D、2 |