题目内容
15.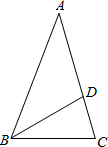 如图,已知△ABC中,AB=AC=2,∠A=36°,∠ABC的平分线BD交AC于点D,则AD的长是-1+$\sqrt{5}$.(结果保留根号)
如图,已知△ABC中,AB=AC=2,∠A=36°,∠ABC的平分线BD交AC于点D,则AD的长是-1+$\sqrt{5}$.(结果保留根号)
分析 可以证明△ABC∽△BDC,设AD=x,根据相似三角形的对应边的比相等,即可列出方程,求得x的值.
解答 解:∵AB=AC=1,∠A=36°,
∴∠ABC=∠ACB=$\frac{180-∠A}{2}$=72°.
∵BD是∠ABC的平分线,
∴∠ABD=∠DBC=$\frac{1}{2}$∠ABC=36°.
∴∠A=∠DBC=36°,
又∵∠C=∠C
∴△ABC∽△BDC,
∴$\frac{AC}{BC}$=$\frac{BC}{CD}$,
设AD=x,则BD=BC=x.则$\frac{2}{x}$=$\frac{x}{2-x}$,
∴x=-1$+\sqrt{5}$,(负值舍去),
∴$AD=-1+\sqrt{5}$.
故答案为:-1$+\sqrt{5}$.
点评 本题考查了等腰三角形的性质,相似三角形的判定和性质,证三角形相似是解题的关键.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
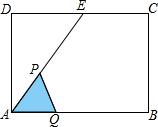 如图,在矩形ABCD中,AB=4cm,AD=2$\sqrt{3}$cm,E为CD边上的中点,点P从点A沿AE运动到点E,点Q从点A沿AB运动到点B时,它们运动的速度都是1cm/s.如果点P,Q同时开始运动,设运动时间为t(s),△APQ的面积为y(cm2),则y与t的函数关系式是y=$\frac{\sqrt{3}}{4}$t2(0<t≤4).
如图,在矩形ABCD中,AB=4cm,AD=2$\sqrt{3}$cm,E为CD边上的中点,点P从点A沿AE运动到点E,点Q从点A沿AB运动到点B时,它们运动的速度都是1cm/s.如果点P,Q同时开始运动,设运动时间为t(s),△APQ的面积为y(cm2),则y与t的函数关系式是y=$\frac{\sqrt{3}}{4}$t2(0<t≤4).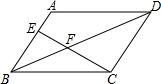 如图,在?ABCD中,E是AB边上的一点,连接CE交对角线BD于F,若AE:BE=2:3,则△BEF和△DCF的周长之比为3:5.
如图,在?ABCD中,E是AB边上的一点,连接CE交对角线BD于F,若AE:BE=2:3,则△BEF和△DCF的周长之比为3:5.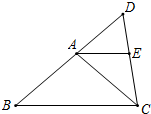 如图,在△ABC中,AB=AC=5cm,∠DCA=∠B,点D在BA延长线上,AE∥BC,交CD于点E,AE=$\frac{25}{8}$cm.
如图,在△ABC中,AB=AC=5cm,∠DCA=∠B,点D在BA延长线上,AE∥BC,交CD于点E,AE=$\frac{25}{8}$cm. 如图,长方形OABC中,O为平面直角坐标系的原点,A点的坐标为(4,0),C点的坐标为(0,5),点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O-C-B-A-O的路线移动(即:沿着长方形移动一周)
如图,长方形OABC中,O为平面直角坐标系的原点,A点的坐标为(4,0),C点的坐标为(0,5),点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O-C-B-A-O的路线移动(即:沿着长方形移动一周)