题目内容
6.已知方程组$\left\{\begin{array}{l}{3x+2y=m+1}\\{2x+y=m-1}\end{array}\right.$,(1)m为何值时,x>y?
(2)求使不等式x-y≤-2成立的正整数m的值.
分析 首先用含有m的代数式分别表示出x,y的值,再根据题意分别列出一元一次不等式进行解答,据此即可得解.
解答 解:$\left\{\begin{array}{l}{3x+2y=m+1①}\\{2x+y=m-1②}\end{array}\right.$,
②×2-①得:x=m-3,
把x=m-3代入①得:3(m-3)+2y=m+1
解得:y=-m+5,
∴原方程组的解是:$\left\{\begin{array}{l}{x=m-3}\\{y=-m+5}\end{array}\right.$
(1)据题意得:m-3>-m+5,
解得:m>4,故:m>4时,x>y;
(2)据题意,得:m-3-(-m+5)≤-2,
解得:m≤3,又因为m是正整数,所以m的值为:1,2,3.
点评 本题主要考查了二元一次方程组的解法,以及一元一次不等式的解法,是比较简单的题目.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
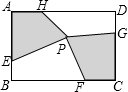 如图,在矩形SBCD中,点E、F、H分别在边AB、BC、CD、DA上,点P在矩形ABCD内,若AB=6,BC=8,AE=CG=4,BF=DH=6,四边形AEPH的面积为11,则四边形PFCG的面积为11.
如图,在矩形SBCD中,点E、F、H分别在边AB、BC、CD、DA上,点P在矩形ABCD内,若AB=6,BC=8,AE=CG=4,BF=DH=6,四边形AEPH的面积为11,则四边形PFCG的面积为11.