题目内容
14.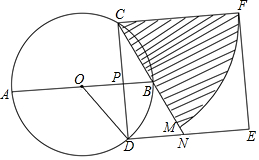 如图,AB是⊙O的直径,CD是⊙O的弦,AB⊥CD,垂足为P,BP:PA=1:3,CD=2$\sqrt{3}$.
如图,AB是⊙O的直径,CD是⊙O的弦,AB⊥CD,垂足为P,BP:PA=1:3,CD=2$\sqrt{3}$.(1)求⊙O的半径;
(2)以CD为边作正方形CDEF,以C为圆心,CF的长为半径画弧交CB的延长线于点M,CB的延长线交DE于点N.
①求阴影部分的面积;
②连接OD,请猜想四边形OBND的形状,并证明你的猜想;
③若正方形CDEF绕着点O旋转一周,求边EF扫过的面积.
分析 (1)先设出BP=x,进而表示出OP=x,在Rt△OPD中,利用勾股定理求出x即可得出结论;
(2)①先利用锐角三角函数求出∠PCB=30°,进而得出∠NCF=60°,再用扇形的面积公式即可;
②先判断出OB∥DN,再利用三角形的中位线判断出OB=DN,得出四边形OBND是平行四边形,最后用半径相等得出四边形OBND是菱形;
③先判断出EF扫过的面积是圆环的面积,即可得出结论.
解答 解:(1)设BP=x,
∵BP:AP=1:3,
∴AP=3x,
∴AB=AP+BP=4x,
∴OD=OB=2x,
∴OP=OB-PB=x,
∵CD⊥AB,
∴CP=DP=$\frac{1}{2}$CD=$\sqrt{3}$,
在Rt△OPD中,根据勾股定理得,OP2+DP2=OD2,
∴x2+3=(2x)2,
∴x=-1(舍)或x=1,
∴⊙O的半径为$\frac{1}{2}$AB=2;
(2)①由(1)知PB=x=1,CP=$\sqrt{3}$,
在Rt△BPC中,tan∠PCB=$\frac{PB}{PC}$=$\frac{1}{\sqrt{3}}$=$\frac{\sqrt{3}}{3}$,
∴∠PCB=30°,
∵四边形CDEF是正方形,
∴CF=CD=2$\sqrt{3}$,∠DCF=90°,
∴∠NCF=90°-30°=60°,
∴S阴影部分=S扇形NCF=$\frac{60π•(2\sqrt{3})^{2}}{360}$=2π;
②四边形OBND是菱形,
理由:∵四边形CDEF是正方形,
∴∠CDE=90°=∠CPB,
∴OB∥DN,
由(1)知,CP=DP,
∴DN=2PB=OB,
∴四边形OBND是平行四边形,
∵OB=OD,
∴?OBND是菱形;
③如图,
连接OF,延长AB交正方形的边EF于G,则OG⊥EF,
∴FG=PC=$\sqrt{3}$,
在Rt△OGF中,OF2=OG2+FG2,
∴OF2-OG2=FG2=3
∴正方形CDEF绕点O旋转一周,边EF扫过的面积=S阴影部分的圆环=π•OF2-π•OG2=π(OF2-OG2)=πFG2=3π.
点评 此题是圆的综合题,主要考查了勾股定理,垂径定理,勾股定理,锐角三角函数,平行四边形的判定,菱形的判定,正方形的性质,三角形的中位线的性质,解(1)的关键是求出x的值,解(2)①的关键是求出∠PCB=30°,解(2)②的关键是判断出四边形OBND是平行四边形,解(2)③的关键是判断出EF扫过的图形是以O为圆心OF和OG为半径的圆环,是一道中等难度的题目.

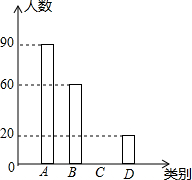 雾霾天气已经成为人们普遍关注的话题,雾霾不仅仅影响人们的出行,还影响着人们的健康.在2017年2月周末休息期间,某校九年级一班综合实践小组的同学以“雾霾天气的主要成因”为主题,随机调查了太原市部分市民的观点,并对调查结果进行了整理,绘制了如下不完整的统计表及统计图,观察并回答下列问题:
雾霾天气已经成为人们普遍关注的话题,雾霾不仅仅影响人们的出行,还影响着人们的健康.在2017年2月周末休息期间,某校九年级一班综合实践小组的同学以“雾霾天气的主要成因”为主题,随机调查了太原市部分市民的观点,并对调查结果进行了整理,绘制了如下不完整的统计表及统计图,观察并回答下列问题:| 类别 | 雾霾天气的主要成因 | 百分比 |
| A | 工业污染 | 45% |
| B | 汽车尾气排放 | m |
| C | 城中村燃煤问题 | 15% |
| D | 其他(绿化不足等) | n |
(2)若该市有800万人口,请你估计持有B,C两类看法的市民共有多少人?
(3)小明同学在四个质地、大小、形状都完全相同的小球上标记A,B,C,D代表四个雾霾天气的主要成因中,放在一个不透明的盒子中,他先随机抽取一个小球,放回去,再随机抽取一个小球,请用画树状图或列表的方法,求出小颖同学刚好抽到B和D的概率.(用A,B,C,D表示各项目)
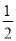 ,则AB的长是____________.
,则AB的长是____________. 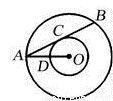
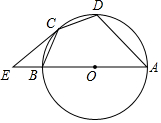 如图,AB为⊙O的直径,$\widehat{CB}$=$\widehat{CD}$,过点C作⊙O的切线交AB的延长线于E,连接BC,CD,AD.
如图,AB为⊙O的直径,$\widehat{CB}$=$\widehat{CD}$,过点C作⊙O的切线交AB的延长线于E,连接BC,CD,AD.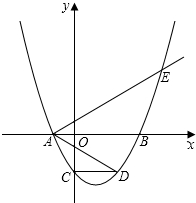 如图,抛物线y=a(x2-2mx-3m2)(其中a,m是常数,且a>0,m>0)与x轴分别交于点A(x1,0),B(x2,0)(点A位于点B的左侧),与y轴交于点C(0,-3),
如图,抛物线y=a(x2-2mx-3m2)(其中a,m是常数,且a>0,m>0)与x轴分别交于点A(x1,0),B(x2,0)(点A位于点B的左侧),与y轴交于点C(0,-3),
 在正方形ABCD中,点E在BC的延长线上,且CE=CD,点F为DE边上一点,连接AF,作FG⊥AF交直线DC于点G
在正方形ABCD中,点E在BC的延长线上,且CE=CD,点F为DE边上一点,连接AF,作FG⊥AF交直线DC于点G