题目内容
19.【感知】如图①,△ABC是等边三角形,点D、E分别在AB、BC边上,且AD=BE,易知:△ADC≌△BEA.【探究】如图②,△ABC是等边三角形,点D、E分别在边BA、CB的延长线上,且AD=BE,△ADC与△BEA还全等吗?如果全等,请证明:如果不全等,请说明理由.
【拓展】如图③,在△ABC中,AB=AC,∠1=∠2,点D、E分别在BA、FB的延长线上,且AD=BE,若AF=$\frac{3}{2}$CF=2BE,S△ABF=6,则S△BCD的大小为13.
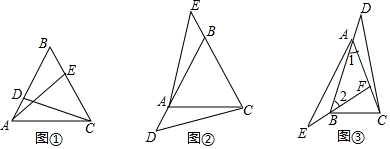
分析 探究:利用平角的定义得出∠DAC=∠EBA即可得出结论;
拓展:先判断出△ADC≌△BEA,进而得出S△ADC=S△BEA,再利用同高的两三角形的面积的比等于底的比求出△ABE,△BCF的面积,即可得出结论.
解答 解:探究:△ADC与△BEA全等,
理由:在等边三角形ABC中,AB=AC,∠BAC=∠ABC=60°,
∴∠DAC=180°-∠BAC=120°,∠EBA=180°-∠ABC=120°,
∴∠DAC=∠EBA,
∵AD=BE,
∴△ADC≌△BEA;
拓展:∵∠1=∠2,
∴AF=BF,∠DAC=∠EBA,
∵AD=BE,AC=AB,
∴△ADC≌△BEA(SAS),
∴S△ADC=S△BEA,
∵AF=2BE,AF=BF,
∴BF=2BE,
∴S△ABE=$\frac{1}{2}$S△ABF=3(同高的两三角形的面积比是底的比),
∴S△ADC=3,
∵AF=$\frac{3}{2}$CF,
∴S△BFC=$\frac{2}{3}$S△ABF=4(同高的两三角形的面积比是底的比),
∴S△BCD=S△BCF+S△ABF+S△ADC=13,
故答案为13.
点评 此题是三角形的综合题,主要考查了等边三角形的性质,等腰三角形的性质,全等三角形的判定和性质,同高的三角形面积的比等于底的比,解探究的关键是得出∠DAC=∠EBA,解拓展的关键是求出△ADC的面积,是一道基础题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
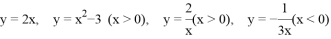 ,将卡片顺序打乱后,随意从中抽取一张,取出的卡片上的函数是
,将卡片顺序打乱后,随意从中抽取一张,取出的卡片上的函数是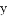 随
随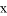 的增大而增大的概率是( )
的增大而增大的概率是( ) B.
B.  C.
C.  D. 1
D. 1
 如图,AB是⊙O的直径,CD是⊙O的弦,AB⊥CD,垂足为P,BP:PA=1:3,CD=2$\sqrt{3}$.
如图,AB是⊙O的直径,CD是⊙O的弦,AB⊥CD,垂足为P,BP:PA=1:3,CD=2$\sqrt{3}$.
 如图,某教学楼AB的后面有一建筑物CD,当光线与地面的夹角是22°时,教学楼在建筑物的墙上留下高2m的影子CE;而当光线与地面夹角是45°时,教学楼顶部A在地面上的影子F与墙角C的距离为18m(B、F、C在同一直线上).求教学楼AB的高;(结果保留整数)(参考数据:sim22°≈0.37,cos22°≈0.93,tan22°≈0.40)
如图,某教学楼AB的后面有一建筑物CD,当光线与地面的夹角是22°时,教学楼在建筑物的墙上留下高2m的影子CE;而当光线与地面夹角是45°时,教学楼顶部A在地面上的影子F与墙角C的距离为18m(B、F、C在同一直线上).求教学楼AB的高;(结果保留整数)(参考数据:sim22°≈0.37,cos22°≈0.93,tan22°≈0.40)