题目内容
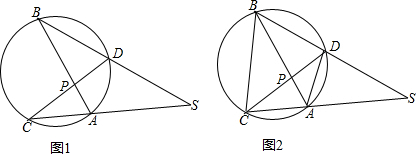
5.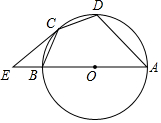 如图,AB为⊙O的直径,$\widehat{CB}$=$\widehat{CD}$,过点C作⊙O的切线交AB的延长线于E,连接BC,CD,AD.
如图,AB为⊙O的直径,$\widehat{CB}$=$\widehat{CD}$,过点C作⊙O的切线交AB的延长线于E,连接BC,CD,AD.(1)求证:∠BCE=$\frac{1}{2}$∠BAD;
(2)若$\frac{CD}{AD}$=$\frac{1}{2}$,求cos∠CBA的值.
分析 (1)先由切线的性质得出∠OCE=90°,再由直径所对的圆周角是直角,即可得出∠ACO=∠BCE,即可得出结论;
(2)先判断出OE是△ABD的中位线,即:OD=$\frac{1}{2}$AD=a,再用勾股定理建立方程得出R=$\frac{1+\sqrt{3}}{2}$a,即可得出结论.
解答 解:(1)如图1, 连接OC,AC,
连接OC,AC,
∵AB是⊙O的直径,
∴∠ACB=90°,
∵CE是⊙O的切线,
∴∠OCE=90°,
∴∠BCE=∠ACO,
∵OA=OC,
∴∠CAB=∠ACO,
∵$\widehat{BC}=\widehat{CD}$,
∴∠CAD=∠CAB,
∴∠CAD=∠ACO=∠BCE,
∴∠BCE=$\frac{1}{2}$∠BAD,
(2)设CD=a,
∴AD=2a,
如图2, 连接BD,OC,AC
连接BD,OC,AC
∵$\widehat{BC}=\widehat{CD}$,
∴BC=CD=a,OC⊥BD,
∵AB是⊙O的直径,
∴∠ADB=90°,
∴OE∥AD,
∵OA=OB,
∴OE=$\frac{1}{2}$AD=a,
设OB=OA=R,
在Rt△BCE中,BE2=a2-(R-a)2,
在Rt△OBE中,BE2=R2-a2,
∴a2-(R-a)2=R2-a2,
∴R=$\frac{1-\sqrt{3}}{2}$a(舍)或R=$\frac{1+\sqrt{3}}{2}$a,
在Rt△ABC中,cos∠ABC=$\frac{BC}{AB}$=$\frac{a}{2R}$=$\frac{a}{(1+\sqrt{3})a}$=$\frac{\sqrt{3}-1}{2}$.
点评 此题考查的是切线的性质,直径所对的圆周角是直角,三角形的中位线的性质,勾股定理,锐角三角函数,解(1)的关键是得出∠BCE=∠ACO,解(2)的关键是用a表示出R,是一道基础题.

 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
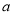 、
、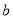 的矩形纸片的四个角都剪去一个边长为
的矩形纸片的四个角都剪去一个边长为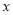 的小正方形.
的小正方形.
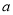 、
、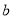 、
、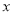 表示纸片剩余部分的面积;
表示纸片剩余部分的面积;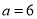 ,
, 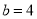 ,且剪去部分的面积等于剩余部分的面积时,求正方形的边长
,且剪去部分的面积等于剩余部分的面积时,求正方形的边长 .
.
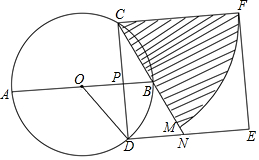 如图,AB是⊙O的直径,CD是⊙O的弦,AB⊥CD,垂足为P,BP:PA=1:3,CD=2$\sqrt{3}$.
如图,AB是⊙O的直径,CD是⊙O的弦,AB⊥CD,垂足为P,BP:PA=1:3,CD=2$\sqrt{3}$.