题目内容
5.已知:等腰三角形ABC的面积为30m2,AB=AC=10m,则底边BC的长度为2$\sqrt{10}$或6$\sqrt{10}$.分析 作CD⊥AB于D,则∠ADC=∠BDC=90°,由三角形的面积求出CD,由勾股定理求出AD;分两种情况:①等腰△ABC为锐角三角形时,求出BD,由勾股定理求出BC即可;②等腰△ABC为钝角三角形时,求出BD,由勾股定理求出BC即可.
解答 解: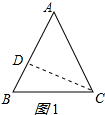 作CD⊥AB于D,
作CD⊥AB于D,
则∠ADC=∠BDC=90°,△ABC的面积=$\frac{1}{2}$AB•CD=$\frac{1}{2}$×10×CD=30,
解得:CD=6,
∴AD=$\sqrt{A{C}^{2}-C{D}^{2}}$=8m;
分两种情况:
①等腰△ABC为锐角三角形时,如图1所示:
BD=AB-AD=2m,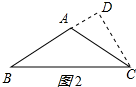
∴BC=$\sqrt{B{D}^{2}+C{D}^{2}}$=2$\sqrt{10}$;
②等腰△ABC为钝角三角形时,如图2所示:
BD=AB+AD=18m,
∴BC=$\sqrt{B{D}^{2}+C{D}^{2}}$=6$\sqrt{10}$;
综上所述:BC的长为2$\sqrt{10}$或6$\sqrt{10}$.
故答案为:2$\sqrt{10}$或6$\sqrt{10}$.
点评 本题考查了等腰三角形的性质、三角形的面积公式及勾股定理,解题的关键画出图形,分两种情况讨论.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16. 如图,在平行四边形ABCD中,下列结论错误的是( )
如图,在平行四边形ABCD中,下列结论错误的是( )
 如图,在平行四边形ABCD中,下列结论错误的是( )
如图,在平行四边形ABCD中,下列结论错误的是( )| A. | ∠ABD=∠BDC | B. | AC⊥BD | C. | AB=CD | D. | ∠BAD=∠BCD |
13. 如图所示的几何体的俯视图是( )
如图所示的几何体的俯视图是( )
 如图所示的几何体的俯视图是( )
如图所示的几何体的俯视图是( )| A. |  | B. |  | C. |  | D. |  |
 如图,在正方形ABCD的外侧,作等边△ADE,则∠EBD=30°.
如图,在正方形ABCD的外侧,作等边△ADE,则∠EBD=30°. 如图,在平面直角坐标系上有点A(1,0),点A第一次向右跳动至A1(-1,1),第二次向左跳动至A2(2,1),第三次向右跳动至A3(-2,2),第四次向左跳动至A4(3,2)…依照此规律跳动下去,点A第2n次跳动至A2n坐标(n+1,n).
如图,在平面直角坐标系上有点A(1,0),点A第一次向右跳动至A1(-1,1),第二次向左跳动至A2(2,1),第三次向右跳动至A3(-2,2),第四次向左跳动至A4(3,2)…依照此规律跳动下去,点A第2n次跳动至A2n坐标(n+1,n).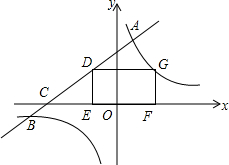 如图,直线y=kx+b与双曲线y=$\frac{3}{x}$相交于点A,B,与x轴相交于点C,矩形DEFG的端点D在直线AB上,E,F在x轴上,点G在双曲线上,若DE=$\frac{3}{2}$,CE=2,点A的横坐标是1.
如图,直线y=kx+b与双曲线y=$\frac{3}{x}$相交于点A,B,与x轴相交于点C,矩形DEFG的端点D在直线AB上,E,F在x轴上,点G在双曲线上,若DE=$\frac{3}{2}$,CE=2,点A的横坐标是1.