Question

6．在等边三角形ABC内有一点P，PA=3，PB=4，PC=5，求正三角形的边长．

Answer 1

分析 将将△APB绕点A逆时针旋转60°得到△ADC，作辅助线，构建直角△AEC，利用图形旋转前后的边长的角度不变，以及等边三角形的性质可以求出∠ADC的度数，从而求得∠CDE=30°，分别计算DE和CE的长，利用勾股定理可以求边长AC．

解答 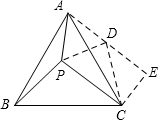解：如图，将△APB绕点A逆时针旋转60°得到△ADC，过C作CE⊥AD，交AD的延长线于E，连接PD，
则AD=PA=3，DC=PB=4，∠PAD=∠BAC=60°，
∴△PAD是等边三角形，
∴PD=3，
在△PDC中，∵PD²+DC²=3²+4²=25，
PC²=5²=25，
∴PD²+DC²=PC²，
∴△PDC是直角三角形，
∴∠PDC=90°，
∴∠ADC=90°+60°=150°，
∴∠CDE=180°-150°=30°，
∴CE=$\frac{1}{2}$CD=2，
由勾股定理得：DE=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$，
∴AE=AD+DE=3+2$\sqrt{3}$，
在Rt△ACE中，AC=$\sqrt{A{E}^{2}+C{E}^{2}}$=$\sqrt{（3+2\sqrt{3}）^{2}+{2}^{2}}$=$\sqrt{25+12\sqrt{3}}$．
答：正三角形的边长为$\sqrt{25+12\sqrt{13}}$．

点评 本题考查了等边三角形的性质、勾股定理的逆定理、旋转的性质，作辅助线构造出直角三角形与全等三角形是解题的关键．本题是通过旋转后得到两三角形全等，则边和角对应相等，并利用勾股定理及其逆定理得出结论．