题目内容
3.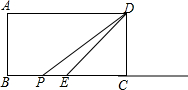 如图.在矩形ABCD中,AB=3.BC=6,DE平分∠ADC交BC于E,点P是射线BC上的动点.
如图.在矩形ABCD中,AB=3.BC=6,DE平分∠ADC交BC于E,点P是射线BC上的动点.(1)当∠ADP=30°,求BP的长;
(2)以点P为圆心,PD为半径的⊙P随点P的运动而变化,当⊙P与四边形ABPD的边(或边所在的直线)相切时,求BP的长.
分析 (1)根据矩形的性质得到CD=AB=3,AD∥BC,由平行线的性质得到∠DPC=∠ADP,由∠ADP=30°,得到∠DPC=30°,根据三角函数的定义即可得到结论;
(2)由题意知,若⊙P与四边形ABPD的边(或边所在的直线)相切时,有以下两种情况:①如图1,当⊙P与AD相切于点D时,有PD⊥AD,即点P与点C重合,根据切线的性质得到PB=BC=6;②当⊙P与AB相切时,根据切线的性质得到∠ABO=90°,然后由勾股定理即可得到结论.
解答 解:(1)在矩形ABCD中,AB=3.BC=6,
∴CD=AB=3,AD∥BC,
∴∠DPC=∠ADP,
∵∠ADP=30°,
∴∠DPC=30°,
∴PC=$\frac{CD}{tan30°}$=$\frac{3}{\frac{\sqrt{3}}{3}}$=3$\sqrt{3}$,
∴PB=BC-PC=6-3$\sqrt{3}$;
(2)由题意知,若⊙P与四边形ABPD的边(或边所在的直线)相切时,有以下两种情况:
①如图1,当⊙P与AD相切于点D时,有PD⊥AD,即点P与点C重合,此时PB=BC=6;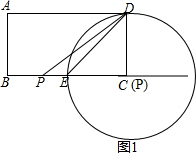
②当⊙P与AB相切时,由题意,得∠ABO=90°,
∴点B为切点,如图2,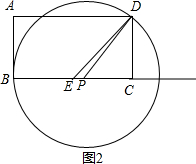
PB2=PD2=PC2+CD2=(6-PB)2+33,
解得:PB=$\frac{15}{4}$,
综上所述:当⊙P与四边形ABPD的边(或边所在的直线)相切时,BP的长为6或$\frac{15}{4}$.
点评 此题考查了切线的性质,坐标与图形性质,勾股定理,等腰直角三角形的判定与性质,锐角三角函数定义,熟练掌握切线的性质是解本题的关键.

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目
12.已知两相似三角形的面积比是4:25,则它们的周长的比为( )
| A. | 4:25 | B. | 2:5 | C. | 1:5 | D. | 以上都不对 |
13.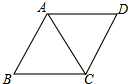 如图,菱形ABCD的边长为6,∠ABC=60°,则对角线AC的长为( )
如图,菱形ABCD的边长为6,∠ABC=60°,则对角线AC的长为( )
 如图,菱形ABCD的边长为6,∠ABC=60°,则对角线AC的长为( )
如图,菱形ABCD的边长为6,∠ABC=60°,则对角线AC的长为( )| A. | 3 | B. | 3$\sqrt{3}$ | C. | 6 | D. | 6$\sqrt{3}$ |
 如图,由几个小正方体组成的立体图形从上面看到几何体的形状是( )
如图,由几个小正方体组成的立体图形从上面看到几何体的形状是( )



 已知a、b、c在数轴上的位置如图所示.
已知a、b、c在数轴上的位置如图所示. 如图,已知△ABC,AB=AC,点D在BA的延长线上,点E在AC上,且AD=AE.
如图,已知△ABC,AB=AC,点D在BA的延长线上,点E在AC上,且AD=AE.