题目内容
4.解方程:$\frac{x-2}{6}-\frac{x+2}{3}=1+\frac{x-1}{2}$.分析 先去分母,再去括号,移项、合并同类项,把x的系数化为1即可.
解答 解:去分母得,x-2-2(x+2)=6+3(x-1),
去括号得,x-2-2x-4=6+3x-3,
移项得,x-2x-3x=6-3+2+4,
合并同类项得,-4x=9,
把x的系数化为1得,x=-$\frac{9}{4}$.
点评 本题考查的是解一元一次方程,熟知解一元一次方程的基本步骤是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14. 已知如图:点A、B、C、D在⊙O上,AB为直径,∠ABC=72°,则∠D为( )
已知如图:点A、B、C、D在⊙O上,AB为直径,∠ABC=72°,则∠D为( )
 已知如图:点A、B、C、D在⊙O上,AB为直径,∠ABC=72°,则∠D为( )
已知如图:点A、B、C、D在⊙O上,AB为直径,∠ABC=72°,则∠D为( )| A. | 18° | B. | 30° | C. | 36° | D. | 72° |
12.把cos12°、sin21°、cos67°、sin69°排列大小正确的是( )
| A. | cos12°<sin21°<cos67°<sin69° | B. | sin21°<cos12°<cos67°<sin69° | ||
| C. | sin21°<cos67°<sin69°<cos12° | D. | cos67°<cos12°<sin21°<sin69° |
9.下列函数中,y是x的二次函数的是( )
| A. | y=2x-1 | B. | y=-$\frac{1}{x}$ | C. | y=2x2-3x+1 | D. | y=$\frac{1}{{{x^2}-2}}$ |
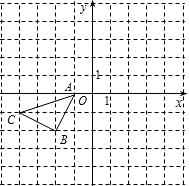 如图所示的正方形网格中,△ABC的顶点均在格点上,在所给直角坐标系中解答下列问题:
如图所示的正方形网格中,△ABC的顶点均在格点上,在所给直角坐标系中解答下列问题: