题目内容
3.已知$\left\{\begin{array}{l}{x=5}\\{y=6}\end{array}\right.$与$\left\{\begin{array}{l}{x=-3}\\{y=-10}\end{array}\right.$都是方程y=kx+b的解,(1)求k,b的值;
(2)若y的值不大于0,求x的取值范围;
(3)若-1≤x<2,求y的取值范围.
分析 (1)把$\left\{\begin{array}{l}{x=5}\\{y=6}\end{array}\right.$与$\left\{\begin{array}{l}{x=-3}\\{y=-10}\end{array}\right.$代入y=kx+b即可求得.
(2)根据k、b的值求得方程,由y的值不大于0,得出2x-4≤0,解得x≤2;
(3)根据不等式的性质即可求得.
解答 解:(1)$\left\{\begin{array}{l}{x=5}\\{y=6}\end{array}\right.$与$\left\{\begin{array}{l}{x=-3}\\{y=-10}\end{array}\right.$代入y=kx+b,得:
$\left\{\begin{array}{l}{5k+b=5}\\{-3k+b=6}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=2}\\{b=-4}\end{array}\right.$;
(2)由(1)得y=2x-4,
∵y≤0,
∴2x-4≤0,解得x≤2;
(3)∵-1≤x<2,
∴-2≤2x<4,
∴-6≤2x-4<0,
即-6≤y<0.
点评 本题考查了解二元一次方程组,解一元一次不等式(组),依据不等式的性质把不等式进行变形是解题的关键.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
13.若x-3y=-5,则代数式5-2x+6y的值是( )
| A. | 0 | B. | 5 | C. | 10 | D. | 15 |
14.某电器按成本价提高30%后标价,再打八折销售,售价为2080元.设该电器的成本价为x元,由题意,下面所列方程正确的是( )
| A. | 80%(1+30%)x=2080 | B. | 30%•80%x=2080 | C. | 2080×30%×80%=x | D. | 30%•x=2080×80% |
18.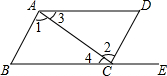 如图,给出下列条件:其中,能推出AB∥DC的是( )
如图,给出下列条件:其中,能推出AB∥DC的是( )
①∠1=∠2; ②∠3=∠4;
③∠B=∠DCE; ④AD∥BC且∠B=∠D.
 如图,给出下列条件:其中,能推出AB∥DC的是( )
如图,给出下列条件:其中,能推出AB∥DC的是( )①∠1=∠2; ②∠3=∠4;
③∠B=∠DCE; ④AD∥BC且∠B=∠D.
| A. | ①④ | B. | ②③ | C. | ①③ | D. | ①③④ |
8.只用下列图形不能镶嵌的是( )
| A. | 正三角形 | B. | 长方形 | C. | 正五边形 | D. | 正六边形 |
12.下列长度的各组线段能组成一个直角三角形的是( )
| A. | 4cm、5cm、11cm | B. | 4cm、5cm、8cm | C. | $\sqrt{3}$cm、$\sqrt{2}$cm、$\sqrt{5}$cm | D. | 2cm、3cm、6cm |
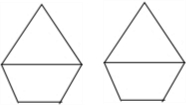 如图是由一个等腰梯形和一个等腰三角形组成的轴对称图形,请你用两种方法作出它的对称轴.(要求:只能用没有刻度的直尺,可不写作法,但要保留作图痕迹)
如图是由一个等腰梯形和一个等腰三角形组成的轴对称图形,请你用两种方法作出它的对称轴.(要求:只能用没有刻度的直尺,可不写作法,但要保留作图痕迹)