题目内容
19.已知$\sqrt{a}$($\sqrt{a}$+$\sqrt{b}$)=3$\sqrt{b}$($\frac{2}{3}$$\sqrt{a}$+4$\sqrt{b}$),其中ab≠0,求$\frac{a-5b+\sqrt{ab}}{a+b+\sqrt{ab}}$.分析 根据二次根式的性质和法则整理原式得a-$\sqrt{ab}$-12b=0,左边因式分解可得$\sqrt{a}$=4$\sqrt{b}$即a=16b,将其代入到代数式中化简计算可得.
解答 解:∵$\sqrt{a}$($\sqrt{a}$+$\sqrt{b}$)=3$\sqrt{b}$($\frac{2}{3}$$\sqrt{a}$+4$\sqrt{b}$),
∴a+$\sqrt{ab}$=2$\sqrt{ab}$+12b,即a-$\sqrt{ab}$-12b=0,
左边因式分解得:($\sqrt{a}$+3$\sqrt{b}$)($\sqrt{a}$-4$\sqrt{b}$)=0,
∵$\sqrt{a}$≥0,$\sqrt{b}$≥0,且ab≠0,
∴$\sqrt{a}$=4$\sqrt{b}$,即a=16b,
则$\frac{a-5b+\sqrt{ab}}{a+b+\sqrt{ab}}$=$\frac{16b-5b+\sqrt{16b•b}}{16b+b+\sqrt{16b•b}}$
=$\frac{11b+4b}{17b+4b}$
=$\frac{15b}{21b}$
=$\frac{5}{7}$.
点评 本题主要考查二次根式的混合运算,熟练掌握二次根式的性质和法则是解题的根本,根据题意因式分解得出a、b间的关系是解题的关键.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
8.如表是某地区某月份的气温数据表,这组数据的中位数和众数分别是( )
| 气温(℃) | 20 | 21 | 22 | 23 | 24 |
| 天数(天) | 4 | 10 | 8 | 6 | 2 |
| A. | 21;21 | B. | 21;21.5 | C. | 21;22 | D. | 22;22 |
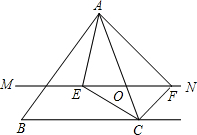 在△ABC中,点O是AC边上的一点,过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角的平分线于点F,连接AE、AF.
在△ABC中,点O是AC边上的一点,过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角的平分线于点F,连接AE、AF.