题目内容
18．把（a-b）$\sqrt{\frac{1}{b-a}}$的根号外的因式移到根号内的结果是-$\sqrt{b-a}$．分析 根据二次根式的乘法，可得答案．
解答 解：原式=-（b-a）$\sqrt{\frac{1}{b-a}}$=-$\sqrt{（b-a）^{2}}$×$\sqrt{\frac{1}{b-a}}$=-$\sqrt{b-a}$．
故答案为：-$\sqrt{b-a}$．
点评 本题考查了二次根式的性质与化简，利用了二次根式的乘法，（a-b）化成-（b-a）是解题关键．
练习册系列答案
相关题目
8．“合家福”超市2015年上半年的营业额与2014年同月营业额相比的增长率如下：
请问：
（1）“合家福”超市2015年上半年的营业额与2014年同月营业额相比，哪个月是增长的？
（2）2015年1月和4月比上年同月增长率是负数，表示什么意思？
（3）2015年上半年与2014年上半年同月份相比营业额没有增长的是哪几个月？
| 月份 | 1 | 2 | 3 | 4 | 5 | 6 |
| 比上年同月增长% | -1.8 | 0 | 0.2 | -1.5 | 0.3 | 0.4 |
（1）“合家福”超市2015年上半年的营业额与2014年同月营业额相比，哪个月是增长的？
（2）2015年1月和4月比上年同月增长率是负数，表示什么意思？
（3）2015年上半年与2014年上半年同月份相比营业额没有增长的是哪几个月？
9．D、E分别是△ABC的边AB、AC上的点，下列各条件中，不能确定DE∥BC的是（ ）
| A． | AD=$\frac{1}{3}$AB，AE=$\frac{1}{3}$AC | B． | $\frac{AE}{AC}$=$\frac{3}{5}$，$\frac{DE}{BC}$=$\frac{3}{5}$ | ||
| C． | $\frac{BD}{AD}$=$\frac{3}{2}$，$\frac{AE}{EC}$=$\frac{2}{3}$ | D． | AD=2，DB=3，AE=3，EC=4$\frac{1}{2}$ |
13．当0＜x＜2时，2$\sqrt{\frac{{x}^{2}+4}{2x}-2}$化简的结果是（ ）
| A． | $\frac{2-x}{x}\sqrt{2x}$ | B． | $\frac{x-2}{x}\sqrt{2x}$ | C． | $\frac{x+2}{2x}\sqrt{2x}$ | D． | $\frac{x+2}{x}\sqrt{2x}$ |
10．已知关于x的方程x2+（6n-m）x+n2+4n+4=0的两个实数根互为相反数，那么m，n的值依次是（ ）
| A． | 12，2 | B． | 6，1 | C． | -12，-2 | D． | 1，$\frac{1}{6}$ |
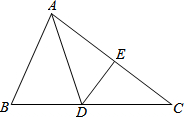如图，在△ABC中，DE⊥AC，垂足为E，∠EAD=∠ECD，AE=3cm，△ABD的周长为13cm，试找出图中相等的线段和相等的角并求出△ABC的周长．
以△ABC的边BC为一边向三角形外侧作正方形BDEC，连结AD、AE分别交BC于点F、G，过点F、G分别作BC的垂线交AB、AC于点H、K，试判断四边形HFGK的形状．