题目内容
13.当0<x<2时,2$\sqrt{\frac{{x}^{2}+4}{2x}-2}$化简的结果是( )| A. | $\frac{2-x}{x}\sqrt{2x}$ | B. | $\frac{x-2}{x}\sqrt{2x}$ | C. | $\frac{x+2}{2x}\sqrt{2x}$ | D. | $\frac{x+2}{x}\sqrt{2x}$ |
分析 根据完全平方公式,可得二次根式的性质,根据二次根式的性质,可得答案.
解答 解:原式=2$\sqrt{\frac{{x}^{2}-4x+4}{2x}}$=2$\sqrt{\frac{(2-x)^{2}•2x}{(2x)^{2}}}$,
当0<x<2时,原式=$\frac{2-x}{x}$$\sqrt{2x}$,
故选:A.
点评 本题考查了二次根式的性质与化简,利用完全平方公式得出二次根式的性质是解题关键.

练习册系列答案
相关题目
3.下列各组有理数的大小比较中,错误的是( )
| A. | -(-$\frac{1}{5}$)$>-\frac{1}{5}$ | B. | -(-3$\frac{2}{5}$)>(-3$\frac{2}{5}$) | C. | -(-4)<+(+4) | D. | +(-1.1)<0 |
2.关于相反数的意义,下列说法正确的是( )
| A. | 一正一负的两个有理数(零除外)称之为相反数 | |
| B. | 具有相反意义的两个数称之为相反数 | |
| C. | 在数轴上原点的两旁,离开原点距离相等的点所表示的两个数 | |
| D. | 符号不同的两个数 |
8.春节前夕,某商店购进了一批衣服,每件衣服的进价为a元,将其价格提高40%后,再以九折出售,则这件衣服的售价是( )
| A. | 0.9a元 | B. | 1.2a元 | C. | 1.26a元 | D. | 1.4a元 |
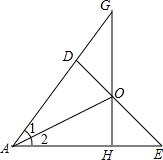 已知,如图,OD⊥AD,OH⊥AE,DE交GH于O.若∠1=∠2,求证:OG=OE.
已知,如图,OD⊥AD,OH⊥AE,DE交GH于O.若∠1=∠2,求证:OG=OE.