题目内容
8.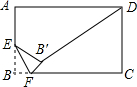 如图,在矩形ABCD中,AB=4,AD=6,E是AB边的中点,F是线段BC边上的动点,将△EBF沿EF所在直线折叠得到△EB′F,连接B′D,则B′D的最小值是2$\sqrt{10}$-2.
如图,在矩形ABCD中,AB=4,AD=6,E是AB边的中点,F是线段BC边上的动点,将△EBF沿EF所在直线折叠得到△EB′F,连接B′D,则B′D的最小值是2$\sqrt{10}$-2.
分析 当∠BFE=∠B'EF,点B′在DE上时,此时B′D的值最小,根据勾股定理求出DE,根据折叠的性质可知B′E=BE=2,即可求出B′D.
解答 解:如图所示: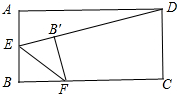 当∠BFE=∠B'EF,点B′在DE上时,此时B′D的值最小,
当∠BFE=∠B'EF,点B′在DE上时,此时B′D的值最小,
根据折叠的性质,△EBF≌△EB′F,
∴EB′⊥B′F,
∴EB′=EB,
∵E是AB边的中点,AB=4,
∴AE=EB′=2,
∵AD=6,
∴DE=$\sqrt{{6}^{2}+{2}^{2}}$=2$\sqrt{10}$,
∴B′D=2$\sqrt{10}$-2.
点评 本题主要考查了折叠的性质、全等三角形的判定与性质、两点之间线段最短的综合运用;确定点B′在何位置时,B′D的值最小是解决问题的关键.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
17.下列四个关系式:(1)y=x;(2)y=x2;(3)y=x3;(4)|y|=x,其中y不是x的函数的是( )
| A. | (1) | B. | (2) | C. | (3) | D. | (4) |
18.下列说法中,错误的是( )
| A. | (-4)2的平方根是-4 | B. | 5是25的算术平方根 | ||
| C. | -$\frac{1}{3}$是-$\frac{1}{27}$的立方根 | D. | -$\frac{5}{6}$是$\frac{25}{36}$的一个平方根 |
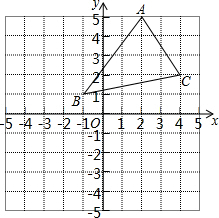 如图,将三角形ABC向左平移3个单位长度,再向下平移4个单位长度,得到三角形A′B′C′,且点A,B,C的对应点分别为点A′,B′,C′.
如图,将三角形ABC向左平移3个单位长度,再向下平移4个单位长度,得到三角形A′B′C′,且点A,B,C的对应点分别为点A′,B′,C′.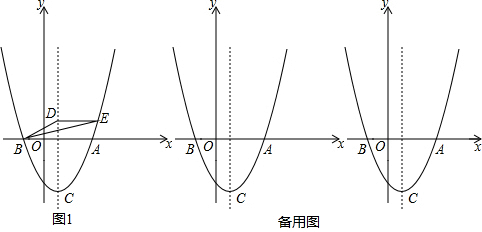
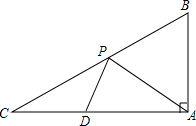 如图,在△ABC中,∠BAC=90°,∠C=30°,AB=$\sqrt{3}$,点D在AC边上,且CD=$\frac{1}{2}$,点P是斜边BC上的一个动点,求PA+PD的最小值.
如图,在△ABC中,∠BAC=90°,∠C=30°,AB=$\sqrt{3}$,点D在AC边上,且CD=$\frac{1}{2}$,点P是斜边BC上的一个动点,求PA+PD的最小值.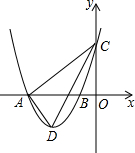 如图,在平面直角坐标系中,抛物线y=ax2+bx+3与x轴交于A(-4,0)、B(-l,0)两点,与y轴交于点C,点D是第三象限的抛物线上一动点.
如图,在平面直角坐标系中,抛物线y=ax2+bx+3与x轴交于A(-4,0)、B(-l,0)两点,与y轴交于点C,点D是第三象限的抛物线上一动点.