题目内容
17.下列四个关系式:(1)y=x;(2)y=x2;(3)y=x3;(4)|y|=x,其中y不是x的函数的是( )| A. | (1) | B. | (2) | C. | (3) | D. | (4) |
分析 根据函数的定义可知,满足对于x的每一个取值,y都有唯一确定的值与之对应关系,据此即可确定不是函数的个数.
解答 解:根据对于x的每一个取值,y都有唯一确定的值与之对应,
(1)y=x,(2)y=x2,(3)y=x3满足函数的定义,y是x的函数,
(4)|y|=x,当x取值时,y不是有唯一的值对应,y不是x的函数,
故选:D.
点评 主要考查了函数的定义.函数的定义:在一个变化过程中,有两个变量x,y,对于x的每一个取值,y都有唯一确定的值与之对应,则y是x的函数,x叫自变量.

练习册系列答案
相关题目
7.下列计算正确的是( )
| A. | a2•a3=a6 | B. | (x+y)2=x2+y2 | C. | (a3b)2=a6b2 | D. | a2÷a3=a(a≠0) |
12.已知$\frac{1}{a}$-$\frac{1}{b}$=4,则$\frac{a-2ab-b}{2a+7ab-2b}$的值等于( )
| A. | 6 | B. | -6 | C. | $\frac{2}{15}$ | D. | -$\frac{2}{7}$ |
6.下列计算,正确的是( )
| A. | $\sqrt{3}$+$\sqrt{2}$=$\sqrt{5}$ | B. | 3$\sqrt{2}$-$\sqrt{2}$=3 | C. | $\sqrt{4}$×$\sqrt{3}$=2$\sqrt{3}$ | D. | $\sqrt{6}$+$\sqrt{3}$=2 |
7. 如图,在坐标系中放置一菱形OABC,已知∠ABC=60°,点B在y轴上,OA=1.将菱形OABC沿x轴的正方向无滑动翻转,每次翻转60°,连续翻转2015次,点B的落点依次为B1,B2,B3,…,则B2015的坐标为( )
如图,在坐标系中放置一菱形OABC,已知∠ABC=60°,点B在y轴上,OA=1.将菱形OABC沿x轴的正方向无滑动翻转,每次翻转60°,连续翻转2015次,点B的落点依次为B1,B2,B3,…,则B2015的坐标为( )
 如图,在坐标系中放置一菱形OABC,已知∠ABC=60°,点B在y轴上,OA=1.将菱形OABC沿x轴的正方向无滑动翻转,每次翻转60°,连续翻转2015次,点B的落点依次为B1,B2,B3,…,则B2015的坐标为( )
如图,在坐标系中放置一菱形OABC,已知∠ABC=60°,点B在y轴上,OA=1.将菱形OABC沿x轴的正方向无滑动翻转,每次翻转60°,连续翻转2015次,点B的落点依次为B1,B2,B3,…,则B2015的坐标为( )| A. | (1343,0) | B. | (1342,0) | C. | (1343.5,$\frac{\sqrt{3}}{2}$) | D. | (1342.5,$\frac{\sqrt{3}}{2}$) |
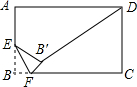 如图,在矩形ABCD中,AB=4,AD=6,E是AB边的中点,F是线段BC边上的动点,将△EBF沿EF所在直线折叠得到△EB′F,连接B′D,则B′D的最小值是2$\sqrt{10}$-2.
如图,在矩形ABCD中,AB=4,AD=6,E是AB边的中点,F是线段BC边上的动点,将△EBF沿EF所在直线折叠得到△EB′F,连接B′D,则B′D的最小值是2$\sqrt{10}$-2. 如图,菱形ABCD的四个顶点都在坐标轴上,A(0,6),B(-6$\sqrt{3}$,0).求S菱形ABCD.
如图,菱形ABCD的四个顶点都在坐标轴上,A(0,6),B(-6$\sqrt{3}$,0).求S菱形ABCD.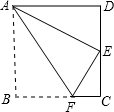 如图,一张矩形纸片ABCD,沿AF折叠,点B恰好落在CD边上的点E处,已知CD为10cm,DE:EC=3:2,则FC的长度为3cm.
如图,一张矩形纸片ABCD,沿AF折叠,点B恰好落在CD边上的点E处,已知CD为10cm,DE:EC=3:2,则FC的长度为3cm.