题目内容
4.已知y是x的反比例函数,且x=3时,y=8.(1)写出y与x之间的函数关系式;
(2)如果自变量x的取值范围为3≤x≤4.求y的取值范围.
分析 (1)根据反比例函数的定义设出表达式,再利用待定系数法解出系数则可;
(2)分别代入x的值求得y值后即可求得y的取值范围;
解答 解:(1)设反比例函数是y=$\frac{k}{x}$(k≠0),
当x=3时,y=8,代入可解得k=24.
所以y=$\frac{24}{x}$.
(2)当x=3时,y=8,当x=4时,y=6,
∴自变量x的取值范围为3≤x≤4.y的取值范围为6≤y≤8.
点评 本题考查了反比例函数的性质及反比例函数的定义,能够利用待定系数法确定反比例函数的解析式是解答本题的关键,难度不大.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
14.若单项式x2ym-n与单项式-$\frac{1}{2}{x^{2m+n}}{y^3}$是同类项,那么这两个多项式的和是( )
| A. | $\frac{1}{2}{x^4}{y^6}$ | B. | $\frac{1}{2}{x^2}{y^3}$ | C. | $\frac{3}{2}{x^2}{y^3}$ | D. | $-\frac{1}{2}{x^2}{y^3}$ |
19.计算(6an+2-9an+1+3an-1)÷3an-1的结果是( )
| A. | 2a3-3a2 | B. | 2a3-3a2+1 | C. | 3a3-6a2+1 | D. | 以上都不对 |
3.若x<0,则|$\sqrt{{x}^{2}}$+3x|=( )
| A. | -4x | B. | 4x | C. | -2x | D. | 2x |
 如图,正方形ABCD中,E为BC中点,DF=$\frac{1}{2}$CF
如图,正方形ABCD中,E为BC中点,DF=$\frac{1}{2}$CF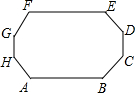 如图,凸八边形ABCDEFGH的8个内角都相等,边AB、BC、CD、DE、EF、FG的长分别为7,4,2,5,6,2,求该八边形的周长.
如图,凸八边形ABCDEFGH的8个内角都相等,边AB、BC、CD、DE、EF、FG的长分别为7,4,2,5,6,2,求该八边形的周长.