题目内容
19.若一元二次方程x2-2x-m=0无实数根,则一次函数y=(m+1)x+m-1的图象不经过第( )象限.| A. | 四 | B. | 三 | C. | 二 | D. | 一 |
分析 根据判别式的意义得到△=(-2)2+4m<0,解得m<-1,然后根据一次函数的性质可得到一次函数y=(m+1)x+m-1图象经过的象限.
解答 解:∵一元二次方程x2-2x-m=0无实数根,
∴△<0,
∴△=4-4(-m)=4+4m<0,
∴m<-1,
∴m+1<1-1,即m+1<0,
m-1<-1-1,即m-1<-2,
∴一次函数y=(m+1)x+m-1的图象不经过第一象限,
故选D.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.也考查了一次函数图象与系数的关系.

练习册系列答案
相关题目
9.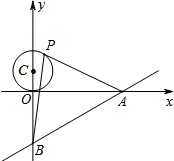 如图,已知直线y=$\frac{3}{4}$x-3与x轴、y轴分别交于A、B两点,P是以C(0,1)为圆心,1为半径的圆上一动点,连结PA、PB.则△PAB面积的最大值是( )
如图,已知直线y=$\frac{3}{4}$x-3与x轴、y轴分别交于A、B两点,P是以C(0,1)为圆心,1为半径的圆上一动点,连结PA、PB.则△PAB面积的最大值是( )
 如图,已知直线y=$\frac{3}{4}$x-3与x轴、y轴分别交于A、B两点,P是以C(0,1)为圆心,1为半径的圆上一动点,连结PA、PB.则△PAB面积的最大值是( )
如图,已知直线y=$\frac{3}{4}$x-3与x轴、y轴分别交于A、B两点,P是以C(0,1)为圆心,1为半径的圆上一动点,连结PA、PB.则△PAB面积的最大值是( )| A. | 8 | B. | 12 | C. | $\frac{21}{2}$ | D. | $\frac{17}{2}$ |
11. 如图,直线l1∥l2,∠1=62°,则∠2的度数为( )
如图,直线l1∥l2,∠1=62°,则∠2的度数为( )
 如图,直线l1∥l2,∠1=62°,则∠2的度数为( )
如图,直线l1∥l2,∠1=62°,则∠2的度数为( )| A. | 152° | B. | 118° | C. | 28° | D. | 62° |
 如图,在△ABC中,DE∥BC,分别交AB,AC于点D、E.若AD=3,DB=2,BC=6,则DE的长为3.6.
如图,在△ABC中,DE∥BC,分别交AB,AC于点D、E.若AD=3,DB=2,BC=6,则DE的长为3.6. 如图,四边形ABCD为矩形,过点D作对角线BD的垂线,交BC的延长线于点E,取BE的中点F,连接DF,DF=4.设AB=x,AD=y,则x2+(y-4)2的值为16.
如图,四边形ABCD为矩形,过点D作对角线BD的垂线,交BC的延长线于点E,取BE的中点F,连接DF,DF=4.设AB=x,AD=y,则x2+(y-4)2的值为16. 如图,已知二次函数y=x2+(1-m)x-m(其中0<m<1)的图象与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,对称轴为直线l.设P为对称轴l上的点,连接PA、PC,PA=PC
如图,已知二次函数y=x2+(1-m)x-m(其中0<m<1)的图象与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,对称轴为直线l.设P为对称轴l上的点,连接PA、PC,PA=PC 如图,已知直线a∥b,∠1=120°,则∠2的度数是60°.
如图,已知直线a∥b,∠1=120°,则∠2的度数是60°.