题目内容
9.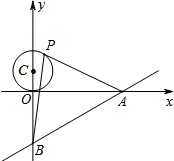 如图,已知直线y=$\frac{3}{4}$x-3与x轴、y轴分别交于A、B两点,P是以C(0,1)为圆心,1为半径的圆上一动点,连结PA、PB.则△PAB面积的最大值是( )
如图,已知直线y=$\frac{3}{4}$x-3与x轴、y轴分别交于A、B两点,P是以C(0,1)为圆心,1为半径的圆上一动点,连结PA、PB.则△PAB面积的最大值是( )| A. | 8 | B. | 12 | C. | $\frac{21}{2}$ | D. | $\frac{17}{2}$ |
分析 求出A、B的坐标,根据勾股定理求出AB,求出点C到AB的距离,即可求出圆C上点到AB的最大距离,根据面积公式求出即可.
解答 解:∵直线y=$\frac{3}{4}$x-3与x轴、y轴分别交于A、B两点,
∴A点的坐标为(4,0),B点的坐标为(0,-3),3x-4y-12=0,
即OA=4,OB=3,由勾股定理得:AB=5,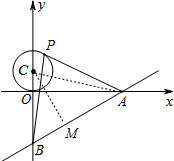
过C作CM⊥AB于M,连接AC,
则由三角形面积公式得:$\frac{1}{2}$×AB×CM=$\frac{1}{2}$×OA×OC+$\frac{1}{2}$×OA×OB,
∴5×CM=4×1+3×4,
∴CM=$\frac{16}{5}$,
∴圆C上点到直线y=$\frac{3}{4}$x-3的最大距离是1+$\frac{16}{5}$=$\frac{21}{5}$,
∴△PAB面积的最大值是$\frac{1}{2}$×5×$\frac{21}{5}$=$\frac{21}{2}$,
故选:C.
点评 本题考查了三角形的面积,点到直线的距离公式的应用,解此题的关键是求出圆上的点到直线AB的最大距离,属于中档题目.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
20.在数轴上表示数-1和2014的两点分别为A和B,则A和B两点间的距离为( )
| A. | 2013 | B. | 2014 | C. | 2015 | D. | 2016 |
4.下列说法不一定成立的是( )
| A. | 若a>b,则a+c>b+c | B. | 若a+c>b+c,则a>b | C. | 若a>b,则ac2>bc2 | D. | 若ac2>bc2,则a>b |
1.已知关于x的一元二次方程3x2+4x-5=0,下列说法正确的是( )
| A. | 方程有两个相等的实数根 | B. | 方程有两个不相等的实数根 | ||
| C. | 没有实数根 | D. | 无法确定 |


 如图,已知三角形ABC的边AB是⊙0的切线,切点为B.AC经过圆心0并与圆相交于点D、C,过C作直线CE丄AB,交AB的延长线于点E.
如图,已知三角形ABC的边AB是⊙0的切线,切点为B.AC经过圆心0并与圆相交于点D、C,过C作直线CE丄AB,交AB的延长线于点E.