题目内容
2．如图，将一条长为7cm的卷尺铺平后折叠，使得卷尺自身的一部分重合，然后在重合部分（阴影处）沿与卷尺边垂直的方向剪一刀，此时卷尺分为了三段，若这三段长度由短到长的比为1：2：4，其中没有完全盖住的部分最长，则折痕对应的刻度可能是2或2.5cm．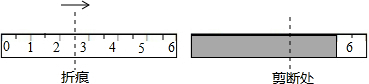
分析 可设折痕对应的刻度为xcm，根据折叠的性质和三段长度由短到长的比为1：2：4，长为7cm的卷尺，列出方程求解即可．
解答 解：设折痕对应的刻度为xcm，依题意有
易知，纸带被剪成了1cm、2cm、4cm三段，又未被盖住的那部分最长，为4cm，所以折痕只能是在1cm的纸带上或2cm的纸带上．
依题意有
①当折痕在2cm的那段上时，2（x-1）=2，解得x=2cm
②当折痕在1cm的那段上时，2（x-2）=1，解得x=2.5cm
故答案为：2或2.5
点评 考查了一元一次方程的应用和图形的剪拼，解题关键是要读懂题目的意思，根据题目给出的条件，找出合适的等量关系列出方程，再求解．注意分类思想的运用．
练习册系列答案
海淀黄冈名师导航系列答案
普通高中同步练习册系列答案
相关题目
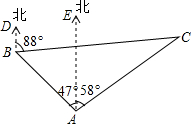某海域有A、B、C三艘船正在捕鱼作业，C船突然出现故障，向A、B两船发出紧急求救信号，此时B船位于A船的北偏西47°方向，距A船26海里的海域，C船位于A船的北偏东58°方向，同时又位于B船的北偏东88°方向．
13．某热播视频10天的点击量达51234.8万次，把它用科学记数法表示是（ ）
| A． | 5.12348×104次 | B． | 0.512348×105次 | C． | 5.12348×108次 | D． | 5.12348×109次 |
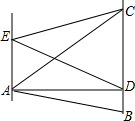如图所示，直线AE∥BD，点C在BD上，若AE=7，BD=3，△ABD的面积为12，求△ACE的面积．
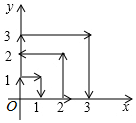一只跳蚤在第一象限及x轴、y轴上跳动，在第一秒钟，它从原点跳动到（0，1），然后接着按图中箭头所示方向跳动[即（0，0）→（0，1）→（1，1）→（1，0）→…]，且每秒跳动一个单位，那么第28秒时跳蚤所在位置的坐标是（3，5）．
15．若不等式ax-2＞0的解集为x＜-2，则关于y的方程ay+2=0的解是（ ）
| A． | y=-1 | B． | y=-2 | C． | y=1 | D． | y=2 |