题目内容
12.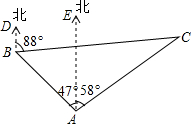 某海域有A、B、C三艘船正在捕鱼作业,C船突然出现故障,向A、B两船发出紧急求救信号,此时B船位于A船的北偏西47°方向,距A船26海里的海域,C船位于A船的北偏东58°方向,同时又位于B船的北偏东88°方向.
某海域有A、B、C三艘船正在捕鱼作业,C船突然出现故障,向A、B两船发出紧急求救信号,此时B船位于A船的北偏西47°方向,距A船26海里的海域,C船位于A船的北偏东58°方向,同时又位于B船的北偏东88°方向.(1)求∠ABC的度数;
(2)A船以每小时40海里的速度前去救援,问多长时间能到出事地点.(结果精确到0.01小时).(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
分析 (1)根据BD∥AE,判断出∠DBA+∠BAE=180°,再求出∠DBA,然后计算∠ABC=133°-88°=45°;
(2))作AH⊥BC于点H,构造直角三角形ACH,利用三角函数解答.
解答  解:(1)∵BD∥AE,
解:(1)∵BD∥AE,
∴∠DBA+∠BAE=180°,
∴∠DBA=180°-47°=133°,
∴∠ABC=133°-88°=45°;
(2)作AH⊥BC于点H,
∴∠C=180°-45°-47°-58°=30°,
∵∠ABC=45°,
∴AH=ABsin45°=13$\sqrt{2}$,
∴AC=2AH=26$\sqrt{2}$.
则A到出事地点的时间是:$\frac{26\sqrt{2}}{40}$≈$\frac{13×1.414}{20}$≈0.92(小时),
答:约0.92小时能到达出事地点.
点评 本题考查了解直角三角形的应用--方向角问题,结合航海中的实际问题,将解直角三角形的相关知识有机结合,体现了数学应用于实际生活的思想.

练习册系列答案
相关题目
17.饭店为某公司提供“白领午餐”,有12元、15元、18元三种价格的套餐可供选择,每人限购一份.本周销售套餐共计500份,其中12元的占总份数的20%,15元的卖出180份,其余均为18元的,那么所购买的盒饭费用的中位数和众数分别是( )
| A. | 15元和18元 | B. | 15元和15元 | C. | 18元和15元 | D. | 18元和18元 |
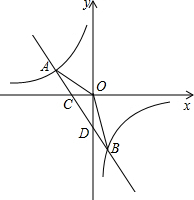 一次函数y=ax+b的图象与反比例函数y=$\frac{k}{x}$的图象交于A,B两点,与x轴交于点C.已知点A(-2,1),点B的坐标为(1,m).
一次函数y=ax+b的图象与反比例函数y=$\frac{k}{x}$的图象交于A,B两点,与x轴交于点C.已知点A(-2,1),点B的坐标为(1,m).