题目内容
3.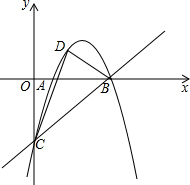 如图,抛物线经过A(1,0),B(4,0),C(0,-4)三点,点D是直线BC上方的抛物线上的一个动点,连结DC,DB,则△BCD的面积的最大值是( )
如图,抛物线经过A(1,0),B(4,0),C(0,-4)三点,点D是直线BC上方的抛物线上的一个动点,连结DC,DB,则△BCD的面积的最大值是( )| A. | 7 | B. | 7.5 | C. | 8 | D. | 9 |
分析 要求△BCD的最大值,只要表示出△BCD的面积即可,根据题目中的信息可以求出抛物线的解析式和直线的解析式,从而可以表示出三角形BCD的面积,从而可以求得△BCD的最大值.
解答 解:设抛物线的解析式是y=ax2+bx+c,
∵抛物线经过A(1,0),B(4,0),C(0,-4)三点,
∴$\left\{\begin{array}{l}{a+b+c=0}\\{16a+4b+c=0}\\{c=-4}\end{array}\right.$
解得,$\left\{\begin{array}{l}{a=-1}\\{b=5}\\{c=-4}\end{array}\right.$
∴y=-x2+5x-4,
设过点B(4,0),C(0,-4)的直线的解析式为y=kx+m
$\left\{\begin{array}{l}{4k+m=0}\\{m=-4}\end{array}\right.$
解得,$\left\{\begin{array}{l}{k=1}\\{m=-4}\end{array}\right.$
即直线BC的直线解析式为:y=x-4,
设点D的坐标是(x,-x2+5x-4)
∴${S}_{△BCD}=\frac{[(-{x}^{2}+5x-4)-(x-4)]×4}{2}$=-2(x-2)2+8,
∴当x=2时,△BCD的面积取得最大值,最大值是8.
故选C.
点评 本题考查二次函数的最值,解题的关键是根据题意求出相应的解析式,可以表示出三角形的面积,运用二次函数最值的相关知识解答.

练习册系列答案
相关题目
13.据统计,2015年到嘉兴市图书馆借阅图书的人约有322万人次.数322万用科学记数法表示为( )
| A. | 3.22×106 | B. | 3.22×105 | C. | 322×104 | D. | 3.22×102 |
14.下列代数式中,属于分式的是( )
| A. | -3 | B. | $\frac{1}{2}a-b$ | C. | $\frac{1}{x}$ | D. | -4a3b |
18.据初步统计,2015年北仑区实现地区生产总值(GDP)约为1134.6亿元.其中1134.6亿元用科学记数法表示为( )
| A. | 1134.6×108元 | B. | 11.346×1010元 | C. | 1.1346×1011元 | D. | 1.1346×1012元 |