题目内容
4.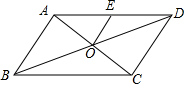 如图,在?ABCD中,对角线AC、BD相交于点O,点E是AD的中点,如果OE=2,AD=6,那么?ABCD的周长是( )
如图,在?ABCD中,对角线AC、BD相交于点O,点E是AD的中点,如果OE=2,AD=6,那么?ABCD的周长是( )| A. | 20 | B. | 12 | C. | 24 | D. | 8 |
分析 由平行四边形的性质和三角形中位线定理得出AB=CD,AD=BC=6,AB=2OE=4,即可得出答案.
解答 解:∵?ABCD对角线相交于点O,E是AD的中点,
∴AB=CD,AD=BC=6,EO是△ABD的中位线,
∴AB=2OE=4,
∴?ABCD的周长=2(AB+AD)=20.
故选:A.
点评 此题主要考查了平行四边形的性质以及三角形中位线定理等知识;求出AB=2OE=4是解题关键.

练习册系列答案
相关题目
15.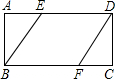 如图,矩形ABCD的AB=4cm,BC=7cm,在AD、BC上分别取点E、F,四边形EBFD是菱形.那么,F到直线BE的距离是( )
如图,矩形ABCD的AB=4cm,BC=7cm,在AD、BC上分别取点E、F,四边形EBFD是菱形.那么,F到直线BE的距离是( )
 如图,矩形ABCD的AB=4cm,BC=7cm,在AD、BC上分别取点E、F,四边形EBFD是菱形.那么,F到直线BE的距离是( )
如图,矩形ABCD的AB=4cm,BC=7cm,在AD、BC上分别取点E、F,四边形EBFD是菱形.那么,F到直线BE的距离是( )| A. | 3cm | B. | 4cm | C. | 5cm | D. | $\sqrt{33}$cm |
12. 将一张两边平行的纸条按如图方式折叠,若∠1=100°,则∠2的度数为( )
将一张两边平行的纸条按如图方式折叠,若∠1=100°,则∠2的度数为( )
 将一张两边平行的纸条按如图方式折叠,若∠1=100°,则∠2的度数为( )
将一张两边平行的纸条按如图方式折叠,若∠1=100°,则∠2的度数为( )| A. | 30° | B. | 40° | C. | 50° | D. | 60° |
19.当x=2时,下列分式中无意义的是( )
| A. | $\frac{x-2}{x}$ | B. | $\frac{x}{x-2}$ | C. | $\frac{x+2}{x}$ | D. | $\frac{x}{x+2}$ |
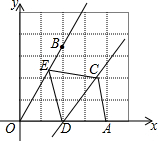 如图,在平面直角坐标系中,点A(4,0),点B(2,2$\sqrt{3}$),点C(2$\sqrt{3}$,2),点D(t,0)是线段OA上一动点,点A关于直线DC的对称点为E.若点E落在∠AOB的外部,则t的取值范围是0<t<2$\sqrt{3}$-2.
如图,在平面直角坐标系中,点A(4,0),点B(2,2$\sqrt{3}$),点C(2$\sqrt{3}$,2),点D(t,0)是线段OA上一动点,点A关于直线DC的对称点为E.若点E落在∠AOB的外部,则t的取值范围是0<t<2$\sqrt{3}$-2. 已知:如图,在△ABC中,AD是BC边上的高,AB=13cm,AC=15cm,AD=12cm,求△ABC的面积.
已知:如图,在△ABC中,AD是BC边上的高,AB=13cm,AC=15cm,AD=12cm,求△ABC的面积.