题目内容
8.如图①,在正方形ABCD中,P是对角线AC上的一点,点E在BC的延长线上,且PE=PB.(1)求证:△BCP≌△DCP;
(2)求证:∠DPE=∠ABC;
(3)把正方形ABCD改为菱形,其它条件不变(如图②),若∠ABC=56°,则∠DPE=56度.(直接填写答案)
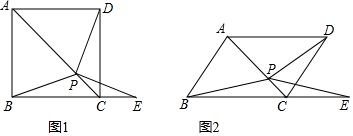
分析 (1)根据正方形的性质得到BC=DC,∠BCP=∠DCP=45°,证明△BCP≌△DCP;
(2)根据全等三角形的性质得到∠CBP=∠CDP,根据等腰三角形的性质得到∠CBP=∠E,证明∠DPE=∠DCE=90°,得到答案;
(3)根据菱形的性质、仿照(2)的证明方法解答即可.
解答 (1)证明:在正方形ABCD中,BC=DC,∠BCP=∠DCP=45°,
在△BCP和△DCP中,
$\left\{\begin{array}{l}{BC=DC}\\{∠BCP=∠DCP}\\{PC=PC}\end{array}\right.$,
∴△BCP≌△DCP(SAS);
(2)证明:由(1)知,△BCP≌△DCP,
∴∠CBP=∠CDP,
∵PE=PB,
∴∠CBP=∠E,
∴∠DPE=∠DCE=90°,
∴∠DPE=∠ABC;
(3)解:在菱形ABCD中,BC=DC,∠BCP=∠DCP,
在△BCP和△DCP中,
$\left\{\begin{array}{l}{BC=DC}\\{∠BCP=∠DCP}\\{PC=PC}\end{array}\right.$,
∴△BCP≌△DCP(SAS),
∴∠CBP=∠CDP,
∵PE=PB,
∴∠CBP=∠E,
∴∠DPE=∠DCE,
∵AB∥CD,
∴∠DCE=∠ABC,
∴∠DPE=∠ABC=56°,
故答案为:56.
点评 本题考查的是正方形的性质、菱形的性质、全等三角形的判定和性质,掌握全等三角形的判定定理和性质定理、正方形和菱形的性质是解题的关键.

练习册系列答案
相关题目
19.四边形ABCD中,AC=BD,顺次连接ABCD各边中点得到的图形为( )
| A. | 平行四边形 | B. | 矩形 | C. | 菱形 | D. | 正方形 |
16.已知点A(x1,y1),B(x2,y2)是反比例函数y=$\frac{1}{x}$图象上的点,若x1>0>x2,则一定成立的是( )
| A. | y1>y2>0 | B. | y1>0>y2 | C. | 0>y1>y2 | D. | y2>0>y1 |
17.下列运算,正确的是( )
| A. | 4a3-a2=3a | B. | a6÷a3=a2 | C. | a2•a3=a5 | D. | (-2a)2=-4a2 |




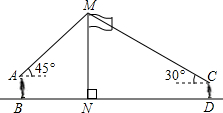 如图,某数学兴趣小组在活动课上测量学校旗杆高度,已知小明的眼睛与地面的距离AB是1.7m,看旗杆顶部M的仰角为45°,小红的眼睛与地面的距离CD是1.5m,看旗杆顶部M的仰角为30°.两人相距23m且位于旗杆两侧(点B,N,D在同一条直线上).请求出旗杆MN的高度.【参考数据:$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7,结果保留整数】
如图,某数学兴趣小组在活动课上测量学校旗杆高度,已知小明的眼睛与地面的距离AB是1.7m,看旗杆顶部M的仰角为45°,小红的眼睛与地面的距离CD是1.5m,看旗杆顶部M的仰角为30°.两人相距23m且位于旗杆两侧(点B,N,D在同一条直线上).请求出旗杆MN的高度.【参考数据:$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7,结果保留整数】