题目内容
9. 如图?ABCD中,AC,BD相交于O,过O点的直线与一组对边分别相交于E,F,图中阴影部分的总面积为2,则?ABCD的面积是( )
如图?ABCD中,AC,BD相交于O,过O点的直线与一组对边分别相交于E,F,图中阴影部分的总面积为2,则?ABCD的面积是( )| A. | 12 | B. | 8 | C. | 6 | D. | 4 |
分析 根据平行四边形的性质得到OA=OC,AB∥CD,AB=DC,BC=AD,∠DAC=∠BCA,根据全等三角形的判定定理得到△AEO≌△CFO,于是得到结论.
解答 解:∵四边形ABCD是平行四边形,
∴OA=OC,AB∥CD,AB=DC,BC=AD,∠DAC=∠BCA,
∴∠AEO=∠CFO,
在△AEO与△CFO中,$\left\{\begin{array}{l}{∠EAO=∠FCO}\\{∠AEO=∠CFO}\\{AO=CO}\end{array}\right.$,
∴△AEO≌△CFO,
∴阴影部分的总面积=S△ABD=$\frac{1}{2}$S四边形ABCD=2,
∴S四边形ABCD=4.
故选D.
点评 题主要考查了平行四边形的性质以及全等三角形的判定和性质,能够根据三角形全等,从而将阴影部分的面积转化为平行四边形面积的一半,是解决问题的关键.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
14.圆有( )条对称轴.
| A. | 1 | B. | 2 | C. | 4 | D. | 无数条 |
1.当代数式x2+3x+5的值为7时,代数式3x2+9x-2的值为( )
| A. | 4 | B. | 2 | C. | -2 | D. | -4 |
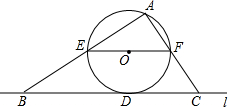 如图,直线L与⊙O相切于点D,半径R=5,过圆心O作EF∥L交⊙O于E、F两点,点A是⊙O上一点,连接AE、AF.并分别延长交直线L于 B、C两点,BD=12,则tan∠ABC=$\frac{5}{7}$.
如图,直线L与⊙O相切于点D,半径R=5,过圆心O作EF∥L交⊙O于E、F两点,点A是⊙O上一点,连接AE、AF.并分别延长交直线L于 B、C两点,BD=12,则tan∠ABC=$\frac{5}{7}$.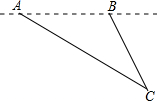 活动一:如图,飞机在距地面9km高空上飞行,先在A处测得正前方某小岛C的俯角为30°,飞行一段距离后,在B处测得该小岛的俯角为60°.求飞机的飞行距离.
活动一:如图,飞机在距地面9km高空上飞行,先在A处测得正前方某小岛C的俯角为30°,飞行一段距离后,在B处测得该小岛的俯角为60°.求飞机的飞行距离.