题目内容
19.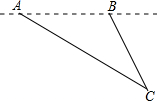 活动一:如图,飞机在距地面9km高空上飞行,先在A处测得正前方某小岛C的俯角为30°,飞行一段距离后,在B处测得该小岛的俯角为60°.求飞机的飞行距离.
活动一:如图,飞机在距地面9km高空上飞行,先在A处测得正前方某小岛C的俯角为30°,飞行一段距离后,在B处测得该小岛的俯角为60°.求飞机的飞行距离.
分析 过点C作CD⊥AB,交AB的延长线于D点,再根据三角形内角和定理得出∠BCA=∠BAC,求出AC和BD的长,最后根据勾股定理求出AD的长,进而得出答案.
解答  解:过点C作CD⊥AB,交AB的延长线于D点,
解:过点C作CD⊥AB,交AB的延长线于D点,
∵∠BAC=30°,∠ADC=90°,
∴∠ACD=60°,
∵∠DBC=60°,
∴∠BCD=30°,
∴∠BCA=30°,
∵CD=9,
∴AC=2CD=18
∴BD=tan30°CD=3$\sqrt{3}$,
∴AD=$\sqrt{A{C}^{2}-C{D}^{2}}$=9$\sqrt{3}$,
∴AB=AD-BD=9$\sqrt{3}$-3$\sqrt{3}$=6$\sqrt{3}$
答:飞机的飞行距离是6$\sqrt{3}$km.
点评 本题考查了解直角三角形的应用,解答本题的关键是根据俯角构造直角三角形,利用三角函数的知识解直角三角形,难度一般.

练习册系列答案
相关题目
8. 如图,∠1与∠2是( )
如图,∠1与∠2是( )
 如图,∠1与∠2是( )
如图,∠1与∠2是( )| A. | 对顶角 | B. | 同位角 | C. | 内错角 | D. | 同旁内角 |
 如图?ABCD中,AC,BD相交于O,过O点的直线与一组对边分别相交于E,F,图中阴影部分的总面积为2,则?ABCD的面积是( )
如图?ABCD中,AC,BD相交于O,过O点的直线与一组对边分别相交于E,F,图中阴影部分的总面积为2,则?ABCD的面积是( )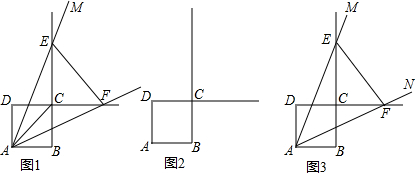
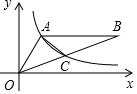 如图,点A(2,3)在反比例函数y=$\frac{k}{x}$(x>0)上,AB∥x轴,连接OB交反比例函数图象于点C,若点C为OB的中点,则S△OAC=4.5.
如图,点A(2,3)在反比例函数y=$\frac{k}{x}$(x>0)上,AB∥x轴,连接OB交反比例函数图象于点C,若点C为OB的中点,则S△OAC=4.5. 如图,小华同学在距离某建筑物6米的点A处测得广告牌B点、C点的仰角分别为52°和35°,则广告牌的高度BC约为( )(精确到0.1米)(sin35°=0.57,cos35°=0.82,tan35°=0.70;sin52°=0.79,cos52°=0.62,tan52°=1.28)
如图,小华同学在距离某建筑物6米的点A处测得广告牌B点、C点的仰角分别为52°和35°,则广告牌的高度BC约为( )(精确到0.1米)(sin35°=0.57,cos35°=0.82,tan35°=0.70;sin52°=0.79,cos52°=0.62,tan52°=1.28)