题目内容
18.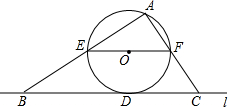 如图,直线L与⊙O相切于点D,半径R=5,过圆心O作EF∥L交⊙O于E、F两点,点A是⊙O上一点,连接AE、AF.并分别延长交直线L于 B、C两点,BD=12,则tan∠ABC=$\frac{5}{7}$.
如图,直线L与⊙O相切于点D,半径R=5,过圆心O作EF∥L交⊙O于E、F两点,点A是⊙O上一点,连接AE、AF.并分别延长交直线L于 B、C两点,BD=12,则tan∠ABC=$\frac{5}{7}$.
分析 连接OD,过E作EH⊥BC,可知四边形EODH为正方形,在Rt△BEH中,可求得tan∠ABC.
解答 解:连接OD,则OD⊥BD,
过E作EH⊥BC,垂足为H,如图,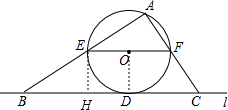
∴EH∥OD,
∵EF∥BC,OE=OD,
∴四边形EODH是正方形,
∴EH=HD=OD=5,
又∵BD=12,
∴BH=7,
在Rt△BEH中,tan∠ABC=$\frac{EH}{BH}$=$\frac{5}{7}$.
点评 本题主要考查切线的性质及正方形的判定和性质、三角函数的定义等知识,掌握切线垂直过切点的半径是解题的关键.

练习册系列答案
相关题目
3.两个实数a、b,规定a?b=$\frac{1}{a}$-b,若1?(x+1)=2,则x的值为( )
| A. | -2 | B. | 1 | C. | -1 | D. | 2 |
8. 如图,∠1与∠2是( )
如图,∠1与∠2是( )
 如图,∠1与∠2是( )
如图,∠1与∠2是( )| A. | 对顶角 | B. | 同位角 | C. | 内错角 | D. | 同旁内角 |
 如图?ABCD中,AC,BD相交于O,过O点的直线与一组对边分别相交于E,F,图中阴影部分的总面积为2,则?ABCD的面积是( )
如图?ABCD中,AC,BD相交于O,过O点的直线与一组对边分别相交于E,F,图中阴影部分的总面积为2,则?ABCD的面积是( )