题目内容
1.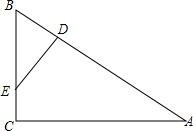 在Rt△ABC中,∠C=90°,D、E分别为AB、BC上的点,且BD•AB=BE•BC.
在Rt△ABC中,∠C=90°,D、E分别为AB、BC上的点,且BD•AB=BE•BC.(1)△ABC与△EBD是否相似,为什么?
(2)ED与AB是否垂直,为什么?
分析 (1)根据两边对应成比例,且夹角相等,两三角形相似即可得到结论;
(2)根据相似三角形的性质即可得到结果.
解答 解:(1)△ABC∽△EBD,理由如下:
∵BD•AB=BE•BC,
∴$\frac{BD}{BC}=\frac{BE}{AB}$,
∵∠CBA=∠EBD
∴△ABC∽△EBD;
(2)ED⊥AB,
理由如下:
由(1)证得△ABC∽△EBD,
∴∠EDA=∠C=90°,
∴ED⊥AB.
点评 本题考查了相似三角形的判定和性质,熟练掌握相似三角形的判定和性质定理是解题的关键.

练习册系列答案
相关题目
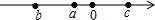 已知实数a,b,c在数轴上的位置如图所示,则化简$\sqrt{{{(a-c)}^2}}+\sqrt{{{(b-a)}^2}}$=c-b.
已知实数a,b,c在数轴上的位置如图所示,则化简$\sqrt{{{(a-c)}^2}}+\sqrt{{{(b-a)}^2}}$=c-b.