题目内容
7.某商店销售一种销售成本为每千克30元的水产品,据市场分析,若按每千克40元销售,一个月能售出500千克;销售单价每涨1元,月销售量就减少10千克,针对这种情况,请解答以下问题:(1)当销售单价定为每千克45元时,计算月销售量和月销售利润;
(2)设销售单价定为每千克x元(x≥40),月销售量为y千克,求y与x的关系式;
(3)该商店想在月销售成本不超过10000元的情况下,使得月销售利润达到8000元,销售单价应定为多少?
分析 (1)根据月销售量为=500-(销售单价-40)×10,即可得出结论,再根据月销售利润=销售每千克的利润×销售数量,代入数据即可得出结论;
(2)根据月销售量=500-10×(销售单价-40),即可得出y与x之间的函数关系式;
(3)先由月销售成本不超过10000元,得出月销售量不超过10000÷30=$\frac{1000}{3}$千克.再根据月销售利润达到8000元列出方程,进而求解即可.
解答 解:(1)当销售单价定为每千克45元时,月销售量为500-(45-40)×10=450(千克),
月销售利润为(45-30)×450=6750(元).
故答案为:450;6750;
(2)根据题意得:y=500-(x-40)×10=-10x+900;
(3)由于月销售成本不超过10000元,
所以月销售量不超过10000÷30=$\frac{1000}{3}$千克.
根据题意得:(x-30)(-10x+900)=8000,
解得:x1=50,x2=70.
当x1=50时,-10×50+900=400>$\frac{1000}{3}$,舍去;
当x2=70时,-10×70+900=200<$\frac{1000}{3}$,符合题意.
故销售单价定为70元.
点评 本题考查了一元二次方程的应用,判断所求的解是否符合题意,舍去不合题意的解.找到关键描述语,找到等量关系准确的列出方程是解决问题的关键.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
18.如图所示,小刚手拿20元钱正在和售货员对话,请你仔细看图,1听果奶、1听可乐的单价分别是( )

| A. | 3元,3.5元 | B. | 3.5元,3元 | C. | 4元,4.5元 | D. | 4.5元,4元 |
12.某校组织学生到距学校6km的光明科技馆参观,准备乘出租车去科技馆,出租车的收费标准如表:
则收费y(元)与出租车行驶里程数x(km)(x≥3)之间的关系式为( )
| 里程数 | 收费/元 |
| 3km以下(含3km) | 8.00 |
| 3km以上每增加1km | 1.80 |
| A. | y=8x | B. | y=1.8x | C. | y=8+1.8x | D. | y=2.6+1.8x |
16. 把一块直尺与一块三角板如图放置,若∠2=130°,则∠1的度数为( )
把一块直尺与一块三角板如图放置,若∠2=130°,则∠1的度数为( )
 把一块直尺与一块三角板如图放置,若∠2=130°,则∠1的度数为( )
把一块直尺与一块三角板如图放置,若∠2=130°,则∠1的度数为( )| A. | 30° | B. | 35° | C. | 40° | D. | 45° |
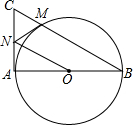 如图,在以AB为直径的⊙O中,过点A作⊙O的切线,点C为切线上一点,连接BC交⊙O于点M,过点M作⊙O的切线交AC于点N,连接ON.
如图,在以AB为直径的⊙O中,过点A作⊙O的切线,点C为切线上一点,连接BC交⊙O于点M,过点M作⊙O的切线交AC于点N,连接ON.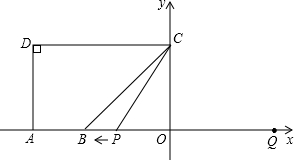 如图,已知A(-5,0)、B(-3,0),点C在y轴的正半轴上,∠CBO=45°,CD∥AB,∠CDA=90°点,P从点Q(4,0)出发,沿x轴向左以每秒1个单位长度的速度运动,运动时间ts.
如图,已知A(-5,0)、B(-3,0),点C在y轴的正半轴上,∠CBO=45°,CD∥AB,∠CDA=90°点,P从点Q(4,0)出发,沿x轴向左以每秒1个单位长度的速度运动,运动时间ts.