题目内容
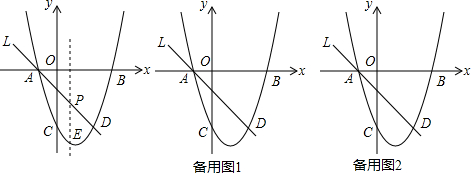
11.如图:抛物线y=x2-2x-3与x轴交于A,B两点,与y轴交于点C,点C关于对称轴的对称点为点D,直线L与抛物线交于点A,D两点.(1)求A,D两点的坐标.
(2)P是线段AD上一个动点,过P做y轴的平行线交抛物线于点E,求线段PE长度最大值.
(3)点M是抛物线上的动点,在x轴上是否存在点N,使以A,D,M,N为顶点的四边形是平行四边形.直接写出所有满足条件的N点坐标.
分析 (1)根据自变量与函数值的对应关系,可得答案;
(2)根据平行于y轴直线上两点间的距离是较大的纵坐标减较小的纵坐标,可得二次函数,根据二次函数的性质,可得答案;
(3)如图4中有四种情形,分别根据平行四边形的性质或利用一次函数的性质解决.
解答 解:(1)当y=0时,x2-2x-3=0,解得x=-1,x=3(不符合题意,舍),即A(-1,0),
当x=0时,y=-3,即C点坐标为(0,-3).
y=x2-2x-3的对称轴为x=1,
由点C关于对称轴的对称点为点D,得D(2,-3);
(2)设直线AD的解析式为y=kx+b,将A、D坐标代入函数解析式,得
y=-x-1.
由P在AD上,E在抛物线上,
设P点坐标为(x,-x-1),E(x,x2-2x-3),
线段PE:y=(-x-1)-(x2-2x-3)=-x2+x+2=-(x-$\frac{1}{2}$)2+$\frac{9}{4}$,
当x=$\frac{1}{2}$,线段PE最大=$\frac{9}{4}$;
(3)如图4中,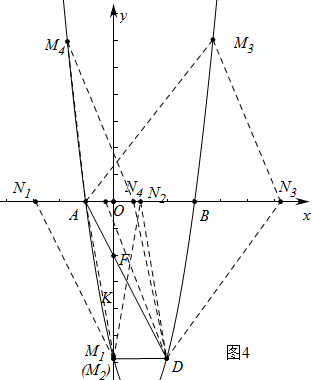 ,
,
①当M1N1∥AD,AN1∥DM1时,AN1=DM1=2,此时N1坐标(-3,0),
②当AD为对角线时,∵AN2=DM2=2,
∴点N2坐标为(1,0),
③当AD∥N3M3,AD=M3N3时,此时点M3的纵坐标为6,当AD∥M4N4,AD=M4N4时,此时点M4的纵坐标为6,
,令y=6,则2x2-4x-6=6,解得x=1±$\sqrt{7}$,
∴M3(1+$\sqrt{7}$,6),M4(1-$\sqrt{7}$,0),
直线M3N3为:y=-2x+8+2$\sqrt{7}$,直线M4N4为:y=-2x+8-2$\sqrt{7}$,
∴N3(4+$\sqrt{7}$,0),N4(4-$\sqrt{7}$,0),
综上所述点N坐标为N1(1,0),N2(-3,0),N3($4+\sqrt{7}$,0),N4($4-\sqrt{7}$,0).
点评 本题考查二次函数的有关知识,学会待定系数法确定函数解析式,解题的关键是会分类讨论,检验是否符合题意,第三个问题需要画出图形,利用平行四边形的性质会一次函数确定点N的坐标,属于中考压轴题.

 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
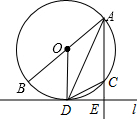 如图所示,已知AB是⊙O的直径,弦AD是∠BAC的平分线,过点D作⊙O的切线l,且AC⊥DE,垂足为点E.
如图所示,已知AB是⊙O的直径,弦AD是∠BAC的平分线,过点D作⊙O的切线l,且AC⊥DE,垂足为点E.