题目内容
13.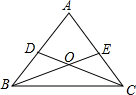 在一次数学课上,周老师在屏幕上出示了一个例题,在△ABC中,D,E分别是AB,AC上的一点,BE与CD交于点O,画出图形(如图),给出下列三个条件:①∠DBO=∠ECO;②BD=CE;③OB=OC.要求同学从这三个等式中选出两个作为已知条件,可判定△ABC是等腰三角形.
在一次数学课上,周老师在屏幕上出示了一个例题,在△ABC中,D,E分别是AB,AC上的一点,BE与CD交于点O,画出图形(如图),给出下列三个条件:①∠DBO=∠ECO;②BD=CE;③OB=OC.要求同学从这三个等式中选出两个作为已知条件,可判定△ABC是等腰三角形.请你用序号在横线上写出其中一种情形,答:①③或①②;并给出证明.
分析 ①③⇒等腰.只要证明∠ABC=∠ACB,即可推出AB=AC;①②⇒等腰.由△DOB≌△EOC(AAS),推出OB=OC即可解决问题;
解答  解:(1)①③⇒等腰
解:(1)①③⇒等腰
理由:∵OB=OC,
∴∠OBC=∠OCB
又∵∠DBE=∠DCE,
∴∠OBC+∠DBE=∠OCB+∠DCE
即∠ABC=∠ACB,
∴AB=AC
(2)①②⇒等腰
理由::在△DOB和△EOC中,
$\left\{\begin{array}{l}∠DOB=∠EOC\\∠OBD=∠OCE\\ BD=CE\end{array}\right.$,
∴△DOB≌△EOC(AAS),
∴OB=OC
由(1)得:AB=AC.
点评 本题考查全等三角形的判定和性质、等腰三角形的判定和性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.

练习册系列答案
相关题目
4.甲、乙、丙三位同学分别正确指出了某一个函数的一个性质.甲:函数图象经过第一象限;乙:函数图象经过第三象限;丙:每第一个象限内,y值随x值的增大而减小.根据他们的描述,这个函数表达式可能是( )
| A. | y=2x | B. | y=$\frac{2}{x}$ | C. | y=-$\frac{1}{x}$ | D. | y=2x2 |
18.$\sqrt{9}+\sqrt{16}$的值是( )
| A. | 7 | B. | -1 | C. | 1 | D. | -7 |
2.若a=355,b=444,c=533,则a,b,c的大小关系是( )
| A. | a>b>c | B. | a>c>b | C. | c>b>a | D. | b>a>c |
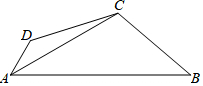 如图,已知四边形ABCD中,AC平分∠DAB,∠DAB=60°,∠B与∠D互补,AC=4,CD=3,则AB-AD=2$\sqrt{5}$.
如图,已知四边形ABCD中,AC平分∠DAB,∠DAB=60°,∠B与∠D互补,AC=4,CD=3,则AB-AD=2$\sqrt{5}$. 已知,如图,∠1=∠2,AB=AE,∠ACB=2∠B.求证:
已知,如图,∠1=∠2,AB=AE,∠ACB=2∠B.求证: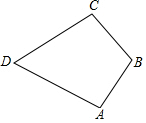 如图,在四边形ABCD中,已知AB=CB,AD=CD,∠ABC=120°,∠ADC=50°,求∠A和∠C的度数.
如图,在四边形ABCD中,已知AB=CB,AD=CD,∠ABC=120°,∠ADC=50°,求∠A和∠C的度数.