题目内容
1.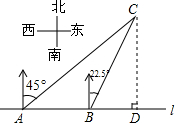 如图,在一笔直的海岸线l上有A、B两个观测站,AB=2km、从A测得船C在北偏东45°的方向,从B测得船C在北偏东22.5°的方向,则船C离海岸线l的距离(即CD的长)为( )
如图,在一笔直的海岸线l上有A、B两个观测站,AB=2km、从A测得船C在北偏东45°的方向,从B测得船C在北偏东22.5°的方向,则船C离海岸线l的距离(即CD的长)为( )| A. | 4km | B. | (2+$\sqrt{2}$)km | C. | 2$\sqrt{2}$km | D. | (4-$\sqrt{2}$)km |
分析 根据题意在CD上取一点E,使BD=DE,设BD=DE=x,则由AD与CD的关系和勾股定理可求得x,从而可求得CD的长.
解答 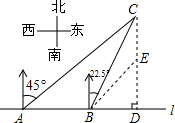 解:在CD上取一点E,使BD=DE,设BD=DE=x.
解:在CD上取一点E,使BD=DE,设BD=DE=x.
∵BD=DE,
∴∠EBD=45°,
由题意可得∠CAD=45°,
∴AD=DC,
∵从B测得船C在北偏东22.5°的方向,
∴∠BCE=∠CBE=22.5°,
∴BE=EC,
∵AB=AD-BD=2km,
∴EC=BE=DC-DE=2km,
∵BD=DE=x,
∴CE=BE=$\sqrt{2}$x,
∴2+x=x+$\sqrt{2}$x,
解得x=$\sqrt{2}$.
∴DC=(2+$\sqrt{2}$)km.
故选:B.
点评 此题主要考查了解直角三角形的应用,得出BE=EC=2是解题关键.

练习册系列答案
 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
16.若m=$\frac{\sqrt{2}}{2}$×(-2),则有( )
| A. | 0<m<1 | B. | -1<m<0 | C. | -2<m<-1 | D. | -3<m<-2 |
10.据有关资料显示,2014年通过国家科技支撑计划,遵义市获得国家级科技专项重点项目资金5533万元,将5533万用科学记数法可表示为( )
| A. | 5.533×108 | B. | 5.533×107 | C. | 5.533×106 | D. | 55.33×106 |
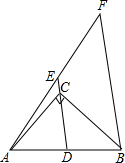 如图,∠ACB=90°,D为AB中点,连接DC并延长到点E,使CE=$\frac{1}{4}$CD,过点B作BF∥DE交AE的延长线于点F.若BF=10,则AB的长为8.
如图,∠ACB=90°,D为AB中点,连接DC并延长到点E,使CE=$\frac{1}{4}$CD,过点B作BF∥DE交AE的延长线于点F.若BF=10,则AB的长为8.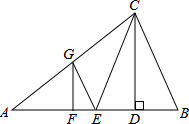 如图,在△ABC中,CD是高,CE是中线,CE=CB,点A、D关于点F对称,过点F作FG∥CD,交AC边于点G,连接GE.若AC=18,BC=12,则△CEG的周长为27.
如图,在△ABC中,CD是高,CE是中线,CE=CB,点A、D关于点F对称,过点F作FG∥CD,交AC边于点G,连接GE.若AC=18,BC=12,则△CEG的周长为27.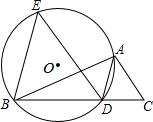 如图,已知AD是△ABC的角平分线,⊙O经过A、B、D三点.过点B作BE∥AD,交⊙O于点E,连接ED
如图,已知AD是△ABC的角平分线,⊙O经过A、B、D三点.过点B作BE∥AD,交⊙O于点E,连接ED