题目内容
6.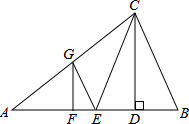 如图,在△ABC中,CD是高,CE是中线,CE=CB,点A、D关于点F对称,过点F作FG∥CD,交AC边于点G,连接GE.若AC=18,BC=12,则△CEG的周长为27.
如图,在△ABC中,CD是高,CE是中线,CE=CB,点A、D关于点F对称,过点F作FG∥CD,交AC边于点G,连接GE.若AC=18,BC=12,则△CEG的周长为27.
分析 先根据点A、D关于点F对称可知点F是AD的中点,再由CD⊥AB,FG∥CD可知FG是△ACD的中位线,故可得出CG的长,再根据点E是AB的中点可知GE是△ABC的中位线,故可得出GE的长,由此可得出结论.
解答 解:∵点A、D关于点F对称,
∴点F是AD的中点.
∵CD⊥AB,FG∥CD,
∴FG是△ACD的中位线,AC=18,BC=12,
∴CG=$\frac{1}{2}$AC=9.
∵点E是AB的中点,
∴GE是△ABC的中位线,
∵CE=CB=12,
∴GE=$\frac{1}{2}$BC=6,
∴△CEG的周长=CG+GE+CE=9+6+12=27.
故答案为:27.
点评 本题考查的是三角形中位线定理,熟知三角形的中位线平行于第三边,并且等于第三边的一半是解答此题的关键.

练习册系列答案
相关题目
14.有一组数据:3,5,5,6,7,这组数据的众数为( )
| A. | 3 | B. | 5 | C. | 6 | D. | 7 |
1.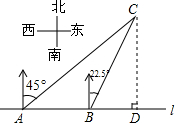 如图,在一笔直的海岸线l上有A、B两个观测站,AB=2km、从A测得船C在北偏东45°的方向,从B测得船C在北偏东22.5°的方向,则船C离海岸线l的距离(即CD的长)为( )
如图,在一笔直的海岸线l上有A、B两个观测站,AB=2km、从A测得船C在北偏东45°的方向,从B测得船C在北偏东22.5°的方向,则船C离海岸线l的距离(即CD的长)为( )
 如图,在一笔直的海岸线l上有A、B两个观测站,AB=2km、从A测得船C在北偏东45°的方向,从B测得船C在北偏东22.5°的方向,则船C离海岸线l的距离(即CD的长)为( )
如图,在一笔直的海岸线l上有A、B两个观测站,AB=2km、从A测得船C在北偏东45°的方向,从B测得船C在北偏东22.5°的方向,则船C离海岸线l的距离(即CD的长)为( )| A. | 4km | B. | (2+$\sqrt{2}$)km | C. | 2$\sqrt{2}$km | D. | (4-$\sqrt{2}$)km |
18.下列立体图形中,俯视图是正方形的是( )
| A. |  | B. |  | C. |  | D. |  |
16.把a2-2a分解因式,正确的是( )
| A. | a(a-2) | B. | a(a+2) | C. | a(a2-2) | D. | a(2-a) |