题目内容
1. 如图,一长方体底面宽AN=5cm,长BN=10cm,高BC=16cm.D为BC的中点,一动点P从A点出发,在长方体表面移动到D点的最短距离是$\sqrt{289}$cm.
如图,一长方体底面宽AN=5cm,长BN=10cm,高BC=16cm.D为BC的中点,一动点P从A点出发,在长方体表面移动到D点的最短距离是$\sqrt{289}$cm.
分析 将图形展开,可得到AD较短的展法两种,通过计算,得到较短的即可.
解答 解:(1)如图1,BD=$\frac{1}{2}$BC=8cm,AB=5+10=15cm,在Rt△ADB中,AD=$\sqrt{{8}^{2}+1{5}^{2}}$=$\sqrt{289}$cm;
(2)如图2,AN=5cm,ND=5+8=13cm,
Rt△ADN中,AD=$\sqrt{A{N}^{2}+D{N}^{2}}$=$\sqrt{{5}^{2}+1{8}^{2}}$=$\sqrt{349}$cm.
综上,动点P从A点出发,在长方体表面移动到D点的最短距离是$\sqrt{289}$cm.
故答案为:$\sqrt{289}$cm.
点评 本题考查了平面展开--最短路径问题,熟悉平面展开图是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.如果5(x-2)与2(3-x)互为相反数,那么x的值是( )
| A. | $\frac{16}{7}$ | B. | $\frac{7}{16}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
17.四个有理数2、1、0、-1,其中最小的是( )
| A. | 1 | B. | 0 | C. | -1 | D. | 2 |
9.如果一个多边形的对角线的条数是边数的一半,那么这个多边形是( )
| A. | 三角形 | B. | 四边形 | C. | 五边形 | D. | 六边形 |
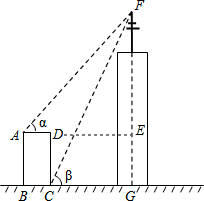 如图,某高楼顶部有一信号发射塔,在矩形建筑物ABCD的A,C两点测得该塔顶端F的仰角分别为和β,矩形建筑物宽度AD=20m,高度DC=33m.求:
如图,某高楼顶部有一信号发射塔,在矩形建筑物ABCD的A,C两点测得该塔顶端F的仰角分别为和β,矩形建筑物宽度AD=20m,高度DC=33m.求: