题目内容
2．已知（a+2）2+|b-$\frac{1}{4}$|=0，求5a2b-[2a2b-（ab2-2a2b）-4]-2ab2的值．分析 原式去括号合并得到最简结果，利用非负数的性质求出x与y的值，代入计算即可求出值．
解答 解：原式=5a2b-2a2b+ab2-2a2b+4-2ab2=a2b-ab2+4，
∵（a+2）2+|b-$\frac{1}{4}$|=0，
∴a=-2，b=$\frac{1}{4}$，
则原式=5$\frac{1}{8}$．
点评 此题考查了整式的加减-化简求值，以及非负数的性质，熟练掌握运算法则是解本题的关键．
练习册系列答案
相关题目
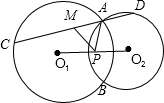设圆O1，圆O2交于点A，B，过A作直线CD交圆O1，圆O2于C，D，M为CD的中点，P为O1O2的中点．求证：PM=PA．
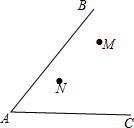如图，南开中学高二年级的学生分别在五云山寨M，N两处参加社会时间活动．先要在道路AB，AC形成的锐角∠BAC内设一个休息区P，使P到两条道路的距离相等，并且使得PM=PN，请用直尺和圆规作出P点的位置（不写作法，值保留作图痕迹）．
7．下列各式中，一定能成立的是（ ）
| A． | $\sqrt{{（-2）}^{2}}$=${（-\sqrt{2}）}^{2}$ | B． | $\sqrt{{（\sqrt{7}-3）}^{2}}$=$\sqrt{7}$-3 | C． | $\sqrt{{x}^{2}+2x+1}$=x+1 | D． | $\sqrt{{x}^{2}-25}$=$\sqrt{x+5}$•$\sqrt{x-5}$ |
11．用两张大小及形状均相同的直角三角形纸片拼图，可拼成（ ）种不同的图形．
| A． | 4 | B． | 5 | C． | 6 | D． | 7 |