题目内容
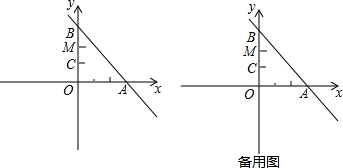
12.如图,一次函数y=-x+3的图象与x,y轴分别交于点A,B,点C、点B关于点M(0,2)对称.(1)求C点坐标;
(2)设过B、C两点的圆的圆心为P
①若P点横坐标为-3,圆P交x轴于点E、F(E在F的左侧),分别求sin∠BEC和sin∠BFC的值;
②对于常数a(a>1),x轴上是否存在点Q,使得sin∠BQC=$\frac{1}{a}$?若存在,求出点Q的坐标;若不存在,请说明理由.
分析 (1)首先求出点A,B的坐标,然后根据点C、点B关于点M(0,2)对称,求出C点坐标是多少即可.
(2)①首先求出圆心的坐标和圆的半径,然后连接BP并延长交⊙P于点G,根据圆周角定理,可得∠BEC=∠BFC=∠BGC,据此求出sin∠BEC和sin∠BFC的值是多少即可.
②x轴上存在点Q,使得sin∠BQC=$\frac{1}{a}$.首先根据sin∠BQC=$\frac{1}{a}$,分别求出圆的半径、圆心的坐标各是多少;然后求出圆的解析式,令y=0,即可求出点Q的坐标.
解答 解:(1)∵一次函数y=-x+3的图象与x,y轴分别交于点A,B,
∴A(3,0)、B(0,3),
又∵点C、点B关于点M(0,2)对称,
∴C点坐标是(0,1).
(2)如图1,连接BP并延长交⊙P于点G, ,
,
∵⊙P过B、C两点,
∴圆心P在BC的中垂线上,
∴P点的纵坐标是2,
又∵P点横坐标为-3,
∴P点坐标为(-3,2),半径r=PB=$\sqrt{{(-3-0)}^{2}{+(2-3)}^{2}}=\sqrt{10}$,
根据圆周角定理,可得
∠BEC=∠BFC=∠BGC,
∵∠BCG=90°,
∴sin∠BEC=sin∠BFC=sin∠BGC=$\frac{BC}{BG}=\frac{3-1}{2\sqrt{10}}$=$\frac{\sqrt{10}}{10}$.
(3)x轴上存在点Q,使得sin∠BQC=$\frac{1}{a}$.
如图2 ,
,
设P(m,2),圆的半径为r,
∵sin∠BQC=$\frac{1}{a}$,
∴$\frac{2}{2r}=\frac{1}{a}$,
∴r=a,
∴$\sqrt{{m}^{2}{+(2-3)}^{2}}=a$,
解得m=$\sqrt{{a}^{2}-1}$或m=-$\sqrt{{a}^{2}-1}$,
∴圆的解析式是${(x+\sqrt{{a}^{2}-1})}^{2}$+(y-2)2=a2或${(x-\sqrt{{a}^{2}-1})}^{2}$+(y-2)2=a2.
①当圆的解析式是${(x+\sqrt{{a}^{2}-1})}^{2}$+(y-2)2=a2时,
令y=0,
可得x=-$\sqrt{{a}^{2}-1}$+$\sqrt{{a}^{2}-4}$或x=-$\sqrt{{a}^{2}-1}$-$\sqrt{{a}^{2}-4}$.
②当圆的解析式是${(x-\sqrt{{a}^{2}-1})}^{2}$+(y-2)2=a2时,
由对称性,可得
可得x=$\sqrt{{a}^{2}-1}$+$\sqrt{{a}^{2}-4}$或x=$\sqrt{{a}^{2}-1}$-$\sqrt{{a}^{2}-4}$.
综上,可得
x轴上存在点Q,使得sin∠BQC=$\frac{1}{a}$,
点Q的坐标是(-$\sqrt{{a}^{2}-1}$+$\sqrt{{a}^{2}-4}$,0)、(-$\sqrt{{a}^{2}-1}$-$\sqrt{{a}^{2}-4}$,0)、($\sqrt{{a}^{2}-1}$+$\sqrt{{a}^{2}-4}$,0)或($\sqrt{{a}^{2}-1}$-$\sqrt{{a}^{2}-4}$,0).
点评 (1)此题主要考查了一次函数综合题,考查了分析推理能力,考查了分类讨论思想的应用,考查了数形结合思想的应用,考查了从已知函数图象中获取信息,并能利用获取的信息解答相应的问题的能力.
(2)此题还考查了圆周角定理的应用,要熟练掌握,解答此题的关键是要明确:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.

 如图,四边形ABCD内接于半径为4的⊙O,BD=4$\sqrt{3}$.
如图,四边形ABCD内接于半径为4的⊙O,BD=4$\sqrt{3}$.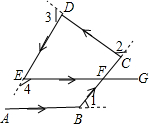 如图,汽车沿“A→B→C→D→E→F”前进过程中,经过四次转弯后与原来方向相同,四次转完的角度分别为∠1、∠2、∠3、∠4,求∠1+∠2+∠3+∠4的度数.
如图,汽车沿“A→B→C→D→E→F”前进过程中,经过四次转弯后与原来方向相同,四次转完的角度分别为∠1、∠2、∠3、∠4,求∠1+∠2+∠3+∠4的度数.