题目内容
10．
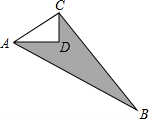如图，已知CD=3，AD=4，∠ADC=90°，BC=12，AB=13．则图中阴影部分的面积=24．
分析 连接AC，利用勾股定理求出AC，求出△ABC是直角三角形，△ABC的面积减去△ACD的面积就是所求的面积．
解答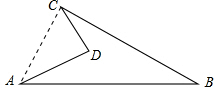 
解：连结AC，
由勾股定理可知
AC=$\sqrt{C{D}^{2}+A{D}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5，
又∵AC2+BC2=52+122=132=AB2，
∴△ABC是直角三角形
故所求面积=S△ABC-S△ACD=$\frac{1}{2}$×5×12-$\frac{1}{2}$×3×4=30-6=24，
故答案为：24．
点评 此题主要考查了直角三角形面积公式以及勾股定理以及逆定理的应用．关键是掌握在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方．
练习册系列答案
小学期末标准试卷系列答案
相关题目
15．
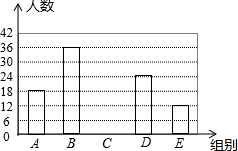随着我市社会经济的发展和交通状况的改善，我市的旅游业得到了高速发展，某旅游公司对我市一企业旅游年消费情况进行了问卷调查，随机抽取部分员工，记录每个人消费金额，并将调查数据适当调整，绘制成如图两幅尚不完整的表和图．
根据以上信息回答下列问题：
（1）a=36，b=0.30，c=120．并将条形统计图补充完整；
（2）这次调查中，个人年消费金额的中位数出现在C组；
（3）若这个企业有3000多名员工，请你估计个人旅游年消费金额在6000元以上的人数．
随着我市社会经济的发展和交通状况的改善，我市的旅游业得到了高速发展，某旅游公司对我市一企业旅游年消费情况进行了问卷调查，随机抽取部分员工，记录每个人消费金额，并将调查数据适当调整，绘制成如图两幅尚不完整的表和图．| 组别 | 个人年消费金额x（元） | 频数（人数） | 频率 |
| A | x≤2000 | 18 | 0.15 |
| B | 2000＜x≤4000 | a | b |
| C | 4000＜x≤6000 | ||
| D | 6000＜x≤8000 | 24 | 0.20 |
| E | x＞8000 | 12 | 0.10 |
| 合计 | c | 1.00 | |
（1）a=36，b=0.30，c=120．并将条形统计图补充完整；
（2）这次调查中，个人年消费金额的中位数出现在C组；
（3）若这个企业有3000多名员工，请你估计个人旅游年消费金额在6000元以上的人数．
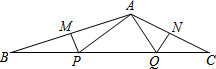如图，△ABC中，∠BAC=135°，点P、Q在边BC上，若MP和QN分别垂直平分AB和AC，并且AP=8，AQ=6，求BC的长．
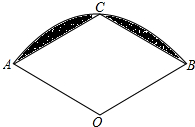如图，在扇形AOB中，半径OA=2，∠AOB=120°，C为弧AB的中点，连接AC、BC，则图中阴影部分的面积是$\frac{4π}{3}$-2$\sqrt{3}$（结果保留π）．
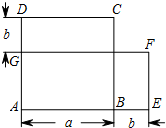（1）如图，正方形ABCD的边长为a，周长为4a；长方形AEFG的长为a+b，宽为a-b，长为4a．
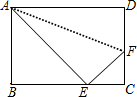如图所示，将矩形ABCD沿直线AF折叠，点D恰好落在边BC上的点E处，若AB=8cm，BC=10cm，求EF的长．