题目内容
1.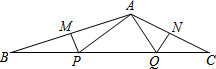 如图,△ABC中,∠BAC=135°,点P、Q在边BC上,若MP和QN分别垂直平分AB和AC,并且AP=8,AQ=6,求BC的长.
如图,△ABC中,∠BAC=135°,点P、Q在边BC上,若MP和QN分别垂直平分AB和AC,并且AP=8,AQ=6,求BC的长.
分析 由MP和QN分别垂直平分AB和AC,根据线段垂直平分线的性质,可得PA=PB,QA=QC,继而可得∠BAP+∠CAQ=∠B+∠C=180°-∠BAC=90°,再利用勾股定理计算出PQ的长,进而可求得答案.
解答 解:∵MP和QN分别垂直平分AB和AC,
∴PA=PB,QA=QC,
∴∠BAP=∠B,∠CAQ=∠C,
∵∠BAC=135°,
∴∠BAP+∠CAQ=∠B+∠C=180°-∠BAC=45°,
∴∠PAQ=∠BAC-(∠BAP+∠CAQ)=90°.
∵AP=8,AQ=6,
∴PQ=$\sqrt{{8}^{2}+{6}^{2}}$=10,
∴BC=20.
点评 此题考查了线段垂直平分线的性质以及等腰三角形的性质.关键是正确计算出∠PAQ的度数,掌握勾股定理.

练习册系列答案
相关题目
6.设x1,x2是方程x2+5x-3=0的两个根,则x12+x22的值是( )
| A. | 19 | B. | 25 | C. | 31 | D. | 30 |
7.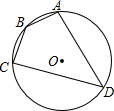 如图,四边形ABCD是⊙O的内接四边形,⊙O的半径为2,∠B=135°,则$\widehat{AC}$的长( )
如图,四边形ABCD是⊙O的内接四边形,⊙O的半径为2,∠B=135°,则$\widehat{AC}$的长( )
 如图,四边形ABCD是⊙O的内接四边形,⊙O的半径为2,∠B=135°,则$\widehat{AC}$的长( )
如图,四边形ABCD是⊙O的内接四边形,⊙O的半径为2,∠B=135°,则$\widehat{AC}$的长( )| A. | 2π | B. | π | C. | $\frac{π}{2}$ | D. | $\frac{π}{3}$ |
9.要使式子$\frac{\sqrt{2-x}}{x-1}$有意义,则x的取值范围是( )
| A. | x≤2 | B. | x≠1 | C. | x≤2或x≠1 | D. | x≤2且x≠1 |
6.若分式$\frac{|x|-3}{x-3}$的值为零,则x=( )
| A. | ±3 | B. | -3 | C. | 3 | D. | 0 |
 如图,D,E,F分别是△ABC的AB,BC,CA边的中点.若△ABC的周长为18cm,则△DEF的周长为9cm.
如图,D,E,F分别是△ABC的AB,BC,CA边的中点.若△ABC的周长为18cm,则△DEF的周长为9cm.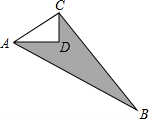 如图,已知CD=3,AD=4,∠ADC=90°,BC=12,AB=13.则图中阴影部分的面积=24.
如图,已知CD=3,AD=4,∠ADC=90°,BC=12,AB=13.则图中阴影部分的面积=24.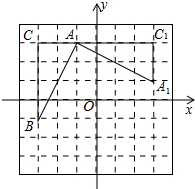 如图,在平面直角坐标系中,有一Rt△ABC,且A(-1,3),B(-3,-1),C(-3,3),已知△A1AC1是由△ABC旋转得到的.
如图,在平面直角坐标系中,有一Rt△ABC,且A(-1,3),B(-3,-1),C(-3,3),已知△A1AC1是由△ABC旋转得到的.